题目内容
在制定投资计划时,不仅要考虑能获得的盈利,而且还要考虑可能出现的亏损.现有甲、乙两个项目进行招商,要求两个项目投资总额不能低于8万元,根据预测,甲、乙项目可能的最大盈利率分别为80%和50%,可能的最大亏损分别为40%和20%.张某现有资金10万元准备投资这两个项目,且要求可能的资金亏损不超过2.6万元.设张某对甲、乙两个项目投资金额分别为x万元和y万元,可能最大盈利为S万元.问:张某对甲、乙两个项目各投资多少万元,才能使可能的盈利最大?并求出盈利的最大值.
考点:简单线性规划的应用
专题:不等式的解法及应用
分析:根据条件建立约束条件,利用数形结合,结合线性规划的应用即可得到结论.
解答:
解:设张某对甲项目投资为x万元,对乙项目投资为y万元,可能最大盈利为S万元,
由题意可知,约束条件为
,
则S=0.8x+0.5y,即y=-1.6x+2S,
画出约束条件的可行域如图:
平移直线y=-1.6x+2S,
右图象可知当直线y=-1.6x+2S经过点M时,直线的截距最大,此时S最大,
由
,解得
,
此时S=0.8×3+0.5×7=5.9,
答:张某对甲投资3万元,乙两个项目投资7万元,才能使可能的盈利最大.盈利的最大值为5.9万元.
由题意可知,约束条件为
|
则S=0.8x+0.5y,即y=-1.6x+2S,
画出约束条件的可行域如图:

平移直线y=-1.6x+2S,
右图象可知当直线y=-1.6x+2S经过点M时,直线的截距最大,此时S最大,
由
|
|
此时S=0.8×3+0.5×7=5.9,
答:张某对甲投资3万元,乙两个项目投资7万元,才能使可能的盈利最大.盈利的最大值为5.9万元.
点评:本题主要考查线性规划的应用,根据条件建立约束条件和目标函数,利用数形结合是解决本题的关键.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
已知函数f(x)=x3+ax2-x+c(x∈R),下列结论错误的是( )
| A、函数f(x)一定存在极大值和极小值 | ||||
B、若函数f(x)在(-∞,x1),(x2,+∞)上是增函数,则x2-x1≥
| ||||
| C、函数f(x)的图象是中心对称图形 | ||||
| D、函数f(x)一定存在三个零点 |
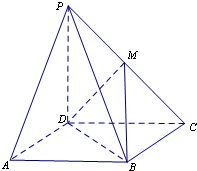 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,点M为PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,点M为PC的中点.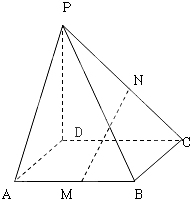 在四棱锥P-ABCD中,PD⊥平面ABCD,底面是边长是1的正方形,M,N分别是AB,PC的中点;
在四棱锥P-ABCD中,PD⊥平面ABCD,底面是边长是1的正方形,M,N分别是AB,PC的中点;
 长方体ABCD-A1B1C1D1中,AB=BC=2a,AA1=a,E,F分别是A1B1和BB1的中点,求EF与AD1所成角的余弦值.
长方体ABCD-A1B1C1D1中,AB=BC=2a,AA1=a,E,F分别是A1B1和BB1的中点,求EF与AD1所成角的余弦值.