题目内容
若函数f(x)=ax3+bx2+cx在x=±1处取得极值,且在x=0处的切线的斜率为-3.
(1)求f(x)的解析式;
(2)若过点A(2,m)可作曲线y=f(x)的2条切线,求实数m的值.
(1)求f(x)的解析式;
(2)若过点A(2,m)可作曲线y=f(x)的2条切线,求实数m的值.
考点:利用导数研究曲线上某点切线方程,函数解析式的求解及常用方法
专题:导数的综合应用
分析:(1)由函数f(x)=ax3+bx2+cx在x=±1处取得极值,且在x=0处的切线的斜率为-3,求导可得±1是f′(x)=0的两根,且f′(0)=-3,解方程组即可求得,a,b,c的值,从而求得f(x)的解析式;
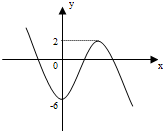
(2)设切点,求切线方程,得到m=-2x03+6x02-6,要求过点A(2,m)可作曲线y=f(x)的2条切线,即求m=-2x03+6x02-6有两个零点,画出函数的草图,即可求得实数m的取值.
(2)设切点,求切线方程,得到m=-2x03+6x02-6,要求过点A(2,m)可作曲线y=f(x)的2条切线,即求m=-2x03+6x02-6有两个零点,画出函数的草图,即可求得实数m的取值.
解答:
 解:(1)f'(x)=3ax2+2bx+c
解:(1)f'(x)=3ax2+2bx+c
依题意
①
又f'(0)=-3,
∴c=-3,
代入①解得a=1,b=0,
∴f(x)=x3-3x;
(2)设切点为(x0,x03-3x0),
∵f'(x)=3x2-3,
∴f'(x0)=3x02-3,
∴切线方程为y-(x03-3x0)=(3x02-3)(x-x0).
又切线过点A(2,m),
∴m-(x03-3x0)=(3x02-3)(2-x0),
∴m=-2x03+6x02-6.
令g(x)=-2x3+6x2-6,
则g'(x)=-6x2+12x=-6x(x-2),
由g'(x)=0,得x=0或x=2,
∴g(x)极小值=g(0)=-6,g(x)极大值=g(2)=2
画出草图知,当m=-6或m=2时,m=-2x3+6x2-6有两解,
即过点A(2,m)可作曲线y=f(x)的2条切线,
∴实数m的取值是-6或2.
 解:(1)f'(x)=3ax2+2bx+c
解:(1)f'(x)=3ax2+2bx+c依题意
|
又f'(0)=-3,
∴c=-3,
代入①解得a=1,b=0,
∴f(x)=x3-3x;
(2)设切点为(x0,x03-3x0),
∵f'(x)=3x2-3,
∴f'(x0)=3x02-3,
∴切线方程为y-(x03-3x0)=(3x02-3)(x-x0).
又切线过点A(2,m),
∴m-(x03-3x0)=(3x02-3)(2-x0),
∴m=-2x03+6x02-6.
令g(x)=-2x3+6x2-6,
则g'(x)=-6x2+12x=-6x(x-2),
由g'(x)=0,得x=0或x=2,
∴g(x)极小值=g(0)=-6,g(x)极大值=g(2)=2
画出草图知,当m=-6或m=2时,m=-2x3+6x2-6有两解,
即过点A(2,m)可作曲线y=f(x)的2条切线,
∴实数m的取值是-6或2.
点评:本题考查利用导数研究函数的单调性和极值问题,考查利用导数研究曲线上某点的切线问题,体现了数形结合的数学思想方法和数学转化思想方法,考查了学生灵活应用知识分析解决问题的能力,是中高档题.

练习册系列答案
相关题目
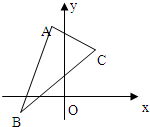 已知△ABC三个顶点是A(-1,4),B(-2,-1),C(2,3).
已知△ABC三个顶点是A(-1,4),B(-2,-1),C(2,3).
 长方体ABCD-A1B1C1D1中,AB=BC=2a,AA1=a,E,F分别是A1B1和BB1的中点,求EF与AD1所成角的余弦值.
长方体ABCD-A1B1C1D1中,AB=BC=2a,AA1=a,E,F分别是A1B1和BB1的中点,求EF与AD1所成角的余弦值. 在某文艺会场中央有一块边长为a米(a为常数)的正方形地面全彩LED显示屏如图所示,点E,F分别为BC,CD边上异于点C的动点.现在顶点A处有视角∠EAF=45°的摄像机,正录制移动区域△ECF内表演的某个文艺节目.设DF=x米,BE=y米.
在某文艺会场中央有一块边长为a米(a为常数)的正方形地面全彩LED显示屏如图所示,点E,F分别为BC,CD边上异于点C的动点.现在顶点A处有视角∠EAF=45°的摄像机,正录制移动区域△ECF内表演的某个文艺节目.设DF=x米,BE=y米.