题目内容
已知函数f(x)=lnx,g(x)=
ax2+bx,a≠0.
(1)若b=2,且函数h(x)=f(x)-g(x)存在单调递减区间,求a的取值范围;
(2)当a=3,b=2时,求函数h(x)=f(x)-g(x)的取值范围.
| 1 |
| 2 |
(1)若b=2,且函数h(x)=f(x)-g(x)存在单调递减区间,求a的取值范围;
(2)当a=3,b=2时,求函数h(x)=f(x)-g(x)的取值范围.
考点:利用导数研究函数的单调性,利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:(1)求函数的解析式和导数,利用函数单调性和导数之间的关系即可得到结论.
(2)求函数的导数,利用函数导数和最值之间的关系即可得到结论.
(2)求函数的导数,利用函数导数和最值之间的关系即可得到结论.
解答:
解:(1)若b=2,则h(x)=f(x)-g(x)=lnx-
ax2-2x,
对函数求导数,得h′(x)=-
(x>0),
依题意,得h′(x)<0在(0,+∞)上有解.
即ax2+2x-1>0在x>0时有解.
∴△=4+4a>0且方程ax2+2x-1=0至少有一个正根.
∴a>-1,
∴a≠0,
∴-1<a<0,或a>0.
(2)当a=3,b=2时,函数h(x)=f(x)-g(x)=lnx-
x2-2x,(x>0),
h′(x)=-
=-
=-
,
由h′(x)>0,解得-1<x<
,此时0<x<
,此时函数单调递增,
由h′(x)<0,解得-1<x<
,此时x>
,此时函数单调递减,
当x=
时,函数取得极大值,同时也是最大值h(
)=ln
-
,
故h(x)=f(x)-g(x)的取值范围是h(x)≤ln
-
.
| 1 |
| 2 |
对函数求导数,得h′(x)=-
| ax2+2x-1 |
| x |
依题意,得h′(x)<0在(0,+∞)上有解.
即ax2+2x-1>0在x>0时有解.
∴△=4+4a>0且方程ax2+2x-1=0至少有一个正根.
∴a>-1,
∴a≠0,
∴-1<a<0,或a>0.
(2)当a=3,b=2时,函数h(x)=f(x)-g(x)=lnx-
| 3 |
| 2 |
h′(x)=-
| ax2+2x-1 |
| x |
| 3x2+2x-1 |
| x |
| (x+1)(3x-1) |
| x |
由h′(x)>0,解得-1<x<
| 1 |
| 3 |
| 1 |
| 3 |
由h′(x)<0,解得-1<x<
| 1 |
| 3 |
| 1 |
| 3 |
当x=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 5 |
| 6 |
故h(x)=f(x)-g(x)的取值范围是h(x)≤ln
| 1 |
| 3 |
| 5 |
| 6 |
点评:本题主要考查导数的应用,利用导数和函数的单调性,最值之间的关系是解决本题的关键.

练习册系列答案
相关题目
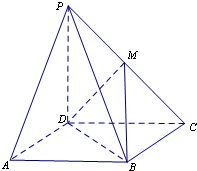 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,点M为PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,点M为PC的中点. 长方体ABCD-A1B1C1D1中,AB=BC=2a,AA1=a,E,F分别是A1B1和BB1的中点,求EF与AD1所成角的余弦值.
长方体ABCD-A1B1C1D1中,AB=BC=2a,AA1=a,E,F分别是A1B1和BB1的中点,求EF与AD1所成角的余弦值. 在某文艺会场中央有一块边长为a米(a为常数)的正方形地面全彩LED显示屏如图所示,点E,F分别为BC,CD边上异于点C的动点.现在顶点A处有视角∠EAF=45°的摄像机,正录制移动区域△ECF内表演的某个文艺节目.设DF=x米,BE=y米.
在某文艺会场中央有一块边长为a米(a为常数)的正方形地面全彩LED显示屏如图所示,点E,F分别为BC,CD边上异于点C的动点.现在顶点A处有视角∠EAF=45°的摄像机,正录制移动区域△ECF内表演的某个文艺节目.设DF=x米,BE=y米.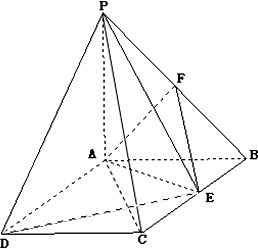 如图:PA⊥平面ABCD,ABCD是矩形,PA=AB=1,点E,F分别是BC,PB的中点.
如图:PA⊥平面ABCD,ABCD是矩形,PA=AB=1,点E,F分别是BC,PB的中点.