题目内容
9．下列各式正确的题目序号有（ ）①log26-log23=log23
②log39=3
③$\root{4}{{{{（-3）}^4}}}=-3$
④20.1＜20.2
⑤log0.72.1＞log0.71.9
⑥${0.9^{\frac{1}{2}}}＞{0.8^{\frac{1}{2}}}$．
| A． | ①④ | B． | ②⑥ | C． | ③⑤ | D． | ④⑥ |
分析 分别根据基本函数的运算性质和函数的单调性判断即可．
解答 解：①log26-log23=log22=1，
②log39=2，
③$\root{4}{（-3）^{4}}$=3，
④20.1＜20.2
⑤log0.72.1＜log0.71.9
⑥${0.9^{\frac{1}{2}}}＞{0.8^{\frac{1}{2}}}$．
故正确的有④⑥，
故选：D．
点评 本题考查了基本函数的运算性质，以及基本函数的单调性，属于基础题．
练习册系列答案
口算小状元口算速算天天练系列答案
相关题目
19．下列函数是正态分布密度函数的是（ ）
| A． | f（x）=$\frac{1}{{\sqrt{2π}σ}}{e^{\frac{{{{（x-r）}^2}}}{2σ}}}$ | B． | f（x）=$\frac{{\sqrt{2π}}}{2π}{e^{-\frac{x^2}{2}}}$ | ||
| C． | f（x）=$\frac{1}{{2\sqrt{2}π}}{e^{\frac{{{{（x-1）}^2}}}{4}}}$ | D． | f（x）=$\frac{1}{{\sqrt{2π}}}{e^{\frac{x^2}{2}}}$ |
20．由2个人在一座8层大楼的底层进入电梯，假设每一个人自第二层开始在每一层离开电梯是等可能的，则这两个人在不同层离开电梯的概率是（ ）
| A． | $\frac{7}{8}$ | B． | $\frac{6}{7}$ | C． | $\frac{5}{6}$ | D． | $\frac{36}{49}$ |
17．已知△ABC的顶点B、C在椭圆$\frac{x^2}{12}+\frac{y^2}{3}=1$上，顶点A是椭圆的一个焦点，且椭圆的另外一个焦点在BC边上，则△ABC的周长是（ ）
| A． | $8\sqrt{3}$ | B． | 6 | C． | $4\sqrt{3}$ | D． | 12 |
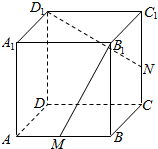如图所示，在正方体ABCD-A1B1C1D1中，M，N分别是线段AB，CC1的中点，∨MB1P的顶点P在棱CC1与棱C1D1上运动，有以下四个命题：
14．下列函数中，既是偶函数又在（0，+∞）上单调递增的是（ ）
| A． | y=x3 | B． | y=|x|+1 | C． | y=-x2+1 | D． | y=（$\frac{1}{2}$）X |