题目内容
12．已知一组数据的频率分布直方图如图所示．求众数、中位数、平均数（ ）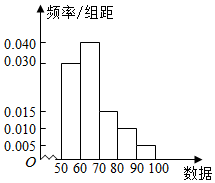
| A． | 63、64、66 | B． | 65、65、67 | C． | 65、64、66 | D． | 64、65、64 |
分析 在频率分布直方图中，众数是最高的小长方形的底边的中点横坐标的值，
中位数是所有小长方形的面积相等的分界线，
平均数是各小长方形底边中点的横坐标与对应频率的积的和，由此求出即可．
解答 解：由频率分布直方图可知，
众数为$\frac{60+70}{2}$=65；
由10×0.03+5×0.04=0.5，所以面积相等的分界线为65，即中位数为65；
平均数为55×0.3+65×0.4+75×0.15+85×0.1+95×0.05=67．
故选：B．
点评 本题考查了利用频率分布直方图求数据的众数、中位数和平均数的问题，是基础题目．
练习册系列答案
相关题目
2．已知f（x）=$\left\{\begin{array}{l}{{2}^{x}+3，x＞0}\\{x-1，x≤0}\end{array}\right.$，则f（1）=（ ）
| A． | 5 | B． | 0 | C． | -5 | D． | 4 |
3．已知向量$\overrightarrow{a}$=（3，-2，1），$\overrightarrow{b}$=（-2，4，0），则4$\overrightarrow{a}$+2$\overrightarrow{b}$等于（ ）
| A． | （16，0，4） | B． | （8，0，4） | C． | （8，16，4） | D． | （8，-16，4） |
20．由2个人在一座8层大楼的底层进入电梯，假设每一个人自第二层开始在每一层离开电梯是等可能的，则这两个人在不同层离开电梯的概率是（ ）
| A． | $\frac{7}{8}$ | B． | $\frac{6}{7}$ | C． | $\frac{5}{6}$ | D． | $\frac{36}{49}$ |
7．已知sin（α+β）=$\frac{1}{2}，sin（α-β）=\frac{1}{10}$，则tanαcotβ=（ ）
| A． | $\frac{3}{2}$ | B． | $\frac{3}{4}$ | C． | $\frac{2}{3}$ | D． | $\frac{4}{3}$ |
17．已知△ABC的顶点B、C在椭圆$\frac{x^2}{12}+\frac{y^2}{3}=1$上，顶点A是椭圆的一个焦点，且椭圆的另外一个焦点在BC边上，则△ABC的周长是（ ）
| A． | $8\sqrt{3}$ | B． | 6 | C． | $4\sqrt{3}$ | D． | 12 |
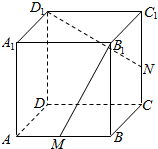如图所示，在正方体ABCD-A1B1C1D1中，M，N分别是线段AB，CC1的中点，∨MB1P的顶点P在棱CC1与棱C1D1上运动，有以下四个命题：