题目内容
19.△ABC中,角A,B,C所对的边分别为a,b,c,且满足3bcosC=3a-c,则cosB=( )| A. | $\frac{2\sqrt{2}}{3}$ | B. | $\frac{1}{3}$ | C. | -$\frac{2\sqrt{2}}{3}$ | D. | -$\frac{1}{3}$ |
分析 利用正弦定理,三角形内角和定理,两角和的正弦函数公式化简已知可得3cosBsinC=sinC,结合sinC≠0,即可解得cosB=$\frac{1}{3}$.
解答 解:∵3bcosC=3a-c,
∴3sinBcosC=3sinA-sinC=3sin(B+C)-sinC=3sinBcosC+3cosBsinC-sinC,
∴3cosBsinC=sinC,
∵C为三角形的内角,sinC≠0,
∴cosB=$\frac{1}{3}$.
故选:B.
点评 本题主要考查了正弦定理,三角形内角和定理,两角和的正弦函数公式在解三角形中的应用,考查了转化思想,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.$\int_2^3{(2x+1)dx=}$( )
| A. | 2 | B. | 6 | C. | 10 | D. | 8 |
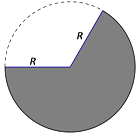 某工厂要生产体积为定值V的漏斗,现选择半径为R的圆形马口铁皮,截取如图所示的扇形,焊制成漏斗.
某工厂要生产体积为定值V的漏斗,现选择半径为R的圆形马口铁皮,截取如图所示的扇形,焊制成漏斗.