题目内容
4.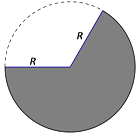 某工厂要生产体积为定值V的漏斗,现选择半径为R的圆形马口铁皮,截取如图所示的扇形,焊制成漏斗.
某工厂要生产体积为定值V的漏斗,现选择半径为R的圆形马口铁皮,截取如图所示的扇形,焊制成漏斗.(1)若漏斗的半径为$\frac{\sqrt{3}}{2}$R,求圆形铁皮的半径R;
(2)这张圆形铁皮的半径R至少是多少?
分析 (1)求出漏斗高,利用体积求圆形铁皮的半径R;
(2)利用导数知识,即可得出结论.
解答 解:(1)漏斗高h=$\frac{1}{2}$R,…(2分)
则体积V=$\frac{1}{3}$π($\frac{\sqrt{3}}{2}$R)2h,所以R=2$\root{3}{\frac{V}{π}}$. …(6分)
(2)设漏斗底面半径为r(r>0),V=$\frac{1}{3}$πr2$\sqrt{{R}^{2}-{r}^{2}}$,R=$\sqrt{\frac{9{V}^{2}}{{π}^{2}{r}^{4}}+{r}^{2}}$,…(9分)
令f(r)=$\frac{9{V}^{2}}{{π}^{2}{r}^{4}}$+r2(r>0),则f′(r)=$\frac{2{π}^{2}{r}^{6}-36{V}^{2}}{{π}^{2}{r}^{5}}$,
所以f(r)在(0,$\root{6}{\frac{18{V}^{2}}{{π}^{2}}}$)上单调减,($\root{6}{\frac{18{V}^{2}}{{π}^{2}}}$,+∞)单调增,…(12分)
所以当r=$\root{6}{\frac{18{V}^{2}}{{π}^{2}}}$时,R取最小值为$\root{3}{\frac{9\sqrt{3}V}{2π}}$.…(15分)
答:这张圆形铁皮的半径R至少为$\root{3}{\frac{9\sqrt{3}V}{2π}}$.…(16分)
点评 本题考查几何中的最值、函数中的最值的求法;考查函数思想;考查阅读理解能力、数学建模的能力、运算能力和叙述表达能力.

练习册系列答案
相关题目
10.已知复数z=i(1+2i),则复数z的虚部为( )
| A. | 2 | B. | 3 | C. | -1 | D. | 1 |
15.在?ABCD中,E是CD上一点,且$\overrightarrow{AE}$=$\frac{1}{2}$$\overrightarrow{AB}$+$\overrightarrow{BC}$,AB=2BC=4,∠BAD=60°,则$\overrightarrow{AC}$•$\overrightarrow{EB}$等于( )
| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | 2 | D. | 3 |
19.△ABC中,角A,B,C所对的边分别为a,b,c,且满足3bcosC=3a-c,则cosB=( )
| A. | $\frac{2\sqrt{2}}{3}$ | B. | $\frac{1}{3}$ | C. | -$\frac{2\sqrt{2}}{3}$ | D. | -$\frac{1}{3}$ |
13.设点P在双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的右支上,双曲线的左、右焦点分别为F1,F2,若|PF1|=4|PF2|,则双曲线离心率的取值范围是( )
| A. | $({1,\frac{5}{3}}]$ | B. | (1,2] | C. | $[{\frac{5}{3},+∞})$ | D. | [2,+∞) |
 在三棱锥E一ABC中,AB⊥AC,AB=1,AC=$\frac{\sqrt{2}}{2}$,点D在线段BC上,且BD=2CD,ED⊥平面ABC.
在三棱锥E一ABC中,AB⊥AC,AB=1,AC=$\frac{\sqrt{2}}{2}$,点D在线段BC上,且BD=2CD,ED⊥平面ABC.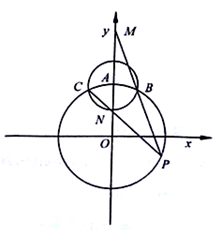 如图,在平面直角坐标系xOy中,圆O:x2+y2=4与y轴的正半轴交于点A,以A为圆心的圆x2+(y-2)2=r2(r>0)与圆O交于B、C两点.
如图,在平面直角坐标系xOy中,圆O:x2+y2=4与y轴的正半轴交于点A,以A为圆心的圆x2+(y-2)2=r2(r>0)与圆O交于B、C两点.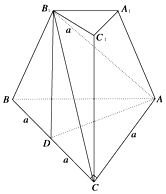 三棱台ABC-A1B1C1中,侧棱CC1⊥底面ABC,∠ACB=90°,AC=B1C1=a,BC=2a,AB1与CC1成45°角,D为BC中点,
三棱台ABC-A1B1C1中,侧棱CC1⊥底面ABC,∠ACB=90°,AC=B1C1=a,BC=2a,AB1与CC1成45°角,D为BC中点,