题目内容
11.已知2a+b-ab=0(a>0,b>0),当ab取得最小值时,曲线$\frac{x|x|}{a}-\frac{y|y|}{b}=1$上的点到直线$y=\sqrt{2}x$的距离的取值范围为(0,$\frac{2\sqrt{6}}{3}$].分析 利用基本不等式可得b=2a=4.再对x,y分类讨论,画出图形,利用直线与曲线相切的性质即可得出.
解答 解:∵2a+b-ab=0(a>0,b>0),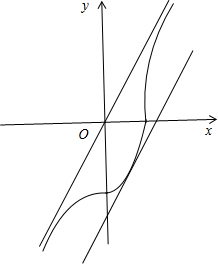
∴ab=2a+b≥2$\sqrt{2ab}$,化为$\sqrt{ab}$($\sqrt{ab}$-2$\sqrt{2}$)≥0,
∴$\sqrt{ab}$≥2$\sqrt{2}$,
解得ab≥8.
当且仅当b=2a=4时取等号.
∴曲线为$\frac{x|x|}{2}$-$\frac{y|y|}{4}$=1.
画出图形:由图形可知:直线y=$\sqrt{2}$x分别是曲线$\frac{{x}^{2}}{2}-\frac{{y}^{2}}{4}$=1,曲线-$\frac{{x}^{2}}{2}$+$\frac{{y}^{2}}{4}$=1的渐近线.因此点到直线y=$\sqrt{2}$x的距离d>0.
设直线y=$\sqrt{2}$x+m与曲线$\frac{{x}^{2}}{2}$+$\frac{{y}^{2}}{4}$=1(x≥0,y≤0)相切.
联立化为$4{x}^{2}+2\sqrt{2}mx+{m}^{2}-4=0$,
令△=8m2-16(m2-4)=0,解得m=-2$\sqrt{2}$.
∴切线为y=$\sqrt{2}x-2\sqrt{2}$.
两平行线y=$\sqrt{2}x-2\sqrt{2}$,y=$\sqrt{2}$x的距离d=$\frac{|0+2\sqrt{2}|}{\sqrt{3}}$=$\frac{2\sqrt{6}}{3}$.
∴曲线$\frac{x|x|}{a}-\frac{y|y|}{b}=1$上的点到直线$y=\sqrt{2}x$的距离取值范围是(0,$\frac{2\sqrt{6}}{3}$].
故答案为(0,$\frac{2\sqrt{6}}{3}$].
点评 本题考查了基本不等式、直线与曲线相切的性质、两点间的距离公式、分类讨论思想方法等基础知识与基本技能方法,考查了推理能力和计算能力,属于难题.

| A. | $\frac{4}{5}$ | B. | $-\frac{4}{5}$ | C. | $\frac{3}{5}$ | D. | $-\frac{3}{5}$ |
| A. | $\frac{2\sqrt{2}}{3}$ | B. | $\frac{1}{3}$ | C. | -$\frac{2\sqrt{2}}{3}$ | D. | -$\frac{1}{3}$ |
| A. | 3 | B. | -4 | C. | 4 | D. | -7 |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
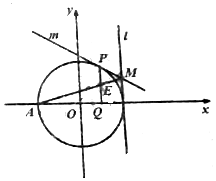 如图,点P是圆O:x2+y2=4上一点,圆O在点P处的切线为m,PQ垂直x轴于点Q(P、Q不重合),线段PQ的重点为E,点A(-2,0),直线l:x=2与直线m交于点M.
如图,点P是圆O:x2+y2=4上一点,圆O在点P处的切线为m,PQ垂直x轴于点Q(P、Q不重合),线段PQ的重点为E,点A(-2,0),直线l:x=2与直线m交于点M.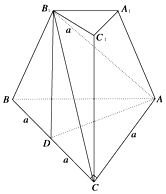 三棱台ABC-A1B1C1中,侧棱CC1⊥底面ABC,∠ACB=90°,AC=B1C1=a,BC=2a,AB1与CC1成45°角,D为BC中点,
三棱台ABC-A1B1C1中,侧棱CC1⊥底面ABC,∠ACB=90°,AC=B1C1=a,BC=2a,AB1与CC1成45°角,D为BC中点,