题目内容

14．要使直线2x-y+5m2=0与直线x+2y-10m=0的交点到直线l：3x-4y-20=0的距离最小，实数m应取何值？这个最小距离是多少？

分析 由直线2x-y+5m2=0与直线x+2y-10m=0，解得交点的坐标，由点到直线的距离公式求出交点到直线l：3x-4y-20=0的距离d，则d是参数m的函数，利用配方法求最值．

解答 解：直线2x-y+5m2=0与直线x+2y-10m=0，解得x=2m-2m2，y=4m+m2．
设两直线交点到直线4x-3y-12=0的距离为d，
则d=$\frac{|6m-6{m}^{2}-16m-4{m}^{2}-20|}{5}$=$\frac{|10（m+\frac{1}{2}）^{2}+\frac{35}{2}|}{5}$
∴当m=-$\frac{1}{2}$时，距离d有最小值为：$\frac{7}{2}$．

点评 本题考查方程思想，考查了点到直线的距离公式，训练了利用配方法求函数的最值，是中档题．

练习册系列答案
相关题目
20．已知$f（α）=\frac{{sin（α-\frac{π}{2}）cos（\frac{3π}{2}+α）tan（π-α）}}{tan（-α-π）sin（-α-π）}，（-\frac{π}{2}＜α＜\frac{π}{2}）$
（Ⅰ）若$cos（α-\frac{3π}{2}）=\frac{1}{5}$，求f（α）的值．
（Ⅱ）若$sin（α-\frac{π}{6}）=-\frac{1}{5}$，求$f（α+\frac{π}{3}）$的值．
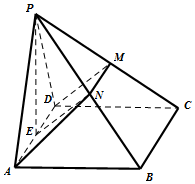5．在四棱锥P-ABCD中，侧面PAD是正三角形，且与底面ABCD垂直，底面ABCD是边长为2的菱形，∠BAD=60°，N是PB的中点，过A、D、N三点的平面交PC于M，E为AD中点．
（Ⅰ）求证：EN∥平面PCD；
（Ⅱ）求证：BC⊥平面PEB；
（Ⅲ）求三棱锥M-PBE的体积．
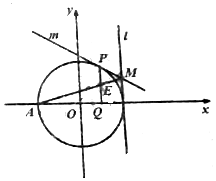2．如图，点P是圆O：x2+y2=4上一点，圆O在点P处的切线为m，PQ垂直x轴于点Q（P、Q不重合），线段PQ的重点为E，点A（-2，0），直线l：x=2与直线m交于点M．
（1）若点P（1，$\sqrt{3}$），求直线m的方程；
（2）当P在圆O上运动时，证明A，E，M三点共线．
9．已知函数g（x）=$\frac{1}{2}$sin（2x+$\frac{2π}{3}$），将其图象向左平移$\frac{π}{4}$个单位，再向上平移$\frac{1}{2}$个单位得到函数f（x）=acos2（x+$\frac{π}{3}$）+b的图象．
（1）求实数a、b的值；
（2）设函数φ（x）=g（x）-$\sqrt{3}$f（x），求函数φ（x）的单调增区间．
19．△ABC中，角A，B，C所对的边分别为a，b，c，且满足3bcosC=3a-c，则cosB=（　　）
A．$\frac{2\sqrt{2}}{3}$B．$\frac{1}{3}$C．-$\frac{2\sqrt{2}}{3}$D．-$\frac{1}{3}$
6．椭圆C1：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的右焦点与抛物线C2：y2=2px（p＞0）的焦点重合，曲线C1与C2相交于点（$\frac{2}{3}$，$\frac{2}{3}$$\sqrt{6}$）．
（I）求椭圆C1的方程；
（II）过右焦点F2的直线l（与x轴不重合）与椭圆C1交于A、C两点，线段AC的中点为G，连接OG并延长交椭圆C1于B点（O为坐标原点），求四边形OABC的面积S的最小值．
3．已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$与直线${l_1}：y=\frac{1}{2}x$，${l_2}：y=-\frac{1}{2}x$，过椭圆上一点P作l1，l2的平行线，分别交l1，l2于M，N两点．若|MN|为定值，则$\sqrt{\frac{a}{b}}$的值是2．
4．《孙子算经》是我国古代数学专著，其中一个问题为“今有出门，望见九堤，堤有九木，木有九枝，枝有九巢，巢有九禽，禽有九雏，雏有九毛，毛有九色”．问：巢有几何？6561．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网