题目内容
已知平面α，β，直线l，m，且有l⊥α，m?β，则下列四个命题正确的个数为（ ）
①若α∥β，则l⊥m； ②若l∥m，则l∥β；
③若α⊥β，则l∥m； ④若l⊥m，则l⊥β．
①若α∥β，则l⊥m； ②若l∥m，则l∥β；
③若α⊥β，则l∥m； ④若l⊥m，则l⊥β．
| A、1 | B、2 | C、3 | D、4 |
考点：空间中直线与平面之间的位置关系
专题：空间位置关系与距离
分析：根据已知中l⊥α，m?β，结合线面垂直的几何特征及面面平行，面面垂直的几何特征及线面平行和线面垂直的判定方法，逐一分析四个结论的真假，可得答案．
解答：
解：若α∥β，则l⊥β，又由m?β，故l⊥m，故①正确；
若l∥m，m?β，则l∥β或l?β，故②错误；
若α⊥β，则l与m相交、平行或异面，故③错误；
若l⊥m，则l与β相交、平行或l?β，故④错误．
故四个命题中正确的命题有1个，
故选A
若l∥m，m?β，则l∥β或l?β，故②错误；
若α⊥β，则l与m相交、平行或异面，故③错误；
若l⊥m，则l与β相交、平行或l?β，故④错误．
故四个命题中正确的命题有1个，
故选A
点评：本题考查的知识点是空间直线与平面之间的位置关系，熟练掌握空间线面关系，面面关系，线线关系的定义，几何特征及性质和判定方法是解答的关键．
练习册系列答案
相关题目
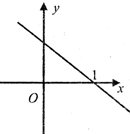函数f（x）的导函数f′（x）的图象是如图所示的一条直线l，l与x轴交点坐标为（1，0），若|a-1|＜|b-1|，则f（a）与f（b）的大小关系为（ ）| A、f（a）＞f（b） |
| B、f（a）＜f（b） |
| C、f（a）=f（b） |
| D、无法确定 |
若x＜0，则2+3x+
的最大值是（ ）
| 4 |
| x |
A、2+4
| ||
B、2±4
| ||
C、2-4
| ||
| D、以上都不对 |
已知平面α内有一个以AB为直径的圆，PA⊥α，点C在圆周上（不同于A、B两点），点D、E分别是点A在PC、PB上的射影，则（ ）
| A、PC⊥面ADE |
| B、∠ACB是二面角A-PC-B的平面角 |
| C、BC∥面ADE |
| D、PB⊥面ADE |