题目内容
若x<0,则2+3x+
的最大值是( )
| 4 |
| x |
A、2+4
| ||
B、2±4
| ||
C、2-4
| ||
| D、以上都不对 |
考点:基本不等式在最值问题中的应用,函数的最值及其几何意义
专题:综合题,不等式的解法及应用
分析:由题意,可变为2+3x+
=2-[(-3x)+(-
)],利用基本不等式求出最值得出正确选项
| 4 |
| x |
| 4 |
| x |
解答:
解:2+3x+
=2-[(-3x)+(-
)],
∵x<0时,(-3x)+(-
)≥2
=4
,
∴2+3x+
=2-[(-3x)+(-
)]≤2-4
,
故x<0时,2+3x+
的最大值是2-4
,
故选:C
| 4 |
| x |
| 4 |
| x |
∵x<0时,(-3x)+(-
| 4 |
| x |
(-3x)×(-
|
| 3 |
∴2+3x+
| 4 |
| x |
| 4 |
| x |
| 3 |
故x<0时,2+3x+
| 4 |
| x |
| 3 |
故选:C
点评:本题考查利用基本不等式求最值,解答时要注意基本不等式等号成立的条件

练习册系列答案
相关题目
若实数x,y满足不等式组
,则|x+y|的最小值为( )
|
| A、3 | B、-1 | C、1 | D、2 |
已知O是锐角△ABC的外心,若
=x
+y
(x,y∈R),则( )
| OC |
| OA |
| OB |
| A、x+y≤-2 |
| B、-2≤x+y<-1 |
| C、x+y<-1 |
| D、-1<x+y<0 |
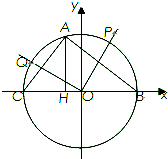 如图,已知B、C是以原点O为圆心,半径为1的圆与x轴的交点,点A在劣弧
如图,已知B、C是以原点O为圆心,半径为1的圆与x轴的交点,点A在劣弧 |
| PQ |
| AH |
| AB |
| AC |
A、(0,
| ||||
B、[
| ||||
C、[
| ||||
D、[
|
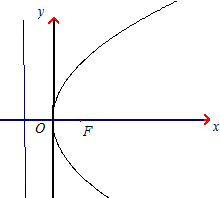 已知抛物线y2=2px(p>0),其焦点为F,一条过焦点F,倾斜角为θ(0<θ<π)的直线交抛物线于A,B两点,连接AO(O为坐标原点),交准线于点B',连接BO,交准线于点A',求四边形ABB'A'的面积.
已知抛物线y2=2px(p>0),其焦点为F,一条过焦点F,倾斜角为θ(0<θ<π)的直线交抛物线于A,B两点,连接AO(O为坐标原点),交准线于点B',连接BO,交准线于点A',求四边形ABB'A'的面积.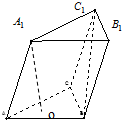 已知三棱柱ABC-A1B1C1的侧棱长和底面边长均为2,A1在底面ABC内的射影O为底面△ABC的中心,如图所示:
已知三棱柱ABC-A1B1C1的侧棱长和底面边长均为2,A1在底面ABC内的射影O为底面△ABC的中心,如图所示: