题目内容
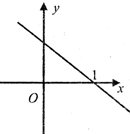 函数f(x)的导函数f′(x)的图象是如图所示的一条直线l,l与x轴交点坐标为(1,0),若|a-1|<|b-1|,则f(a)与f(b)的大小关系为( )
函数f(x)的导函数f′(x)的图象是如图所示的一条直线l,l与x轴交点坐标为(1,0),若|a-1|<|b-1|,则f(a)与f(b)的大小关系为( )| A、f(a)>f(b) |
| B、f(a)<f(b) |
| C、f(a)=f(b) |
| D、无法确定 |
考点:利用导数研究函数的单调性
专题:导数的概念及应用
分析:由导函数的图象是一条直线,知道原函数是二次函数,再根据导数的正负性,得出对称轴和开口方向,由二次函数的性质即可得出答案.
解答:
解:由f′(x)图象为一直线l,知f(x)是一个二次函数,
又∵当x∈(-∞,1)时f′(x)>0,f(x)单调递增,当x∈(1,+∞)时,f′(x)<0,f(x)单调递减;
∴f(x)的对称轴为x=1,且抛物线的开口向下,
又∵|a-1|<|b-1|,
∴a与对称轴较近,
∴f(a)>f(b).
故选:A.
又∵当x∈(-∞,1)时f′(x)>0,f(x)单调递增,当x∈(1,+∞)时,f′(x)<0,f(x)单调递减;
∴f(x)的对称轴为x=1,且抛物线的开口向下,
又∵|a-1|<|b-1|,
∴a与对称轴较近,
∴f(a)>f(b).
故选:A.
点评:本题考查了函数与导数的性质,二次函数的性质特点,属于基础题.

练习册系列答案
相关题目
若实数x,y满足不等式组
,则|x+y|的最小值为( )
|
| A、3 | B、-1 | C、1 | D、2 |
执行如图所示的程序框图,则输出的结果是( )


| A、5 | B、7 | C、9 | D、11 |
已知O是锐角△ABC的外心,若
=x
+y
(x,y∈R),则( )
| OC |
| OA |
| OB |
| A、x+y≤-2 |
| B、-2≤x+y<-1 |
| C、x+y<-1 |
| D、-1<x+y<0 |
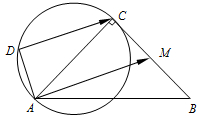 如图,已知:|AC|=|BC|=4,∠ACB=90°,M为BC的中点,D为以AC为直径的圆上一动点,则
如图,已知:|AC|=|BC|=4,∠ACB=90°,M为BC的中点,D为以AC为直径的圆上一动点,则