题目内容
某学生在高考前1个月买了一本数学《高考冲刺压轴卷》,每套试卷中有10道选择题,每道选择题有4个选项,其中有且仅有一个选项正确.评分标准是“每题仅选一个选项,选对得5分,不选或选错得零分”.假设该生在压轴卷(一)的选择题中确定能做对前6题,第7-9题每题只能排除两个选项是错误的,第10题完全不能理解题意,只能随意猜测.
(1)求该生选择题得满分的概率;
(2)设该学生选择题的得分为X,求X的分布列和数学期望EX,若该生要想每次选择题的平均得分不少于40分,这样才有更大的机会使整卷得到高分120分以上,问是否还应继续努力以提高正确率?
(1)求该生选择题得满分的概率;
(2)设该学生选择题的得分为X,求X的分布列和数学期望EX,若该生要想每次选择题的平均得分不少于40分,这样才有更大的机会使整卷得到高分120分以上,问是否还应继续努力以提高正确率?
考点:离散型随机变量的期望与方差,互斥事件的概率加法公式
专题:综合题,概率与统计
分析:(1)由题意,该学生必可答对前6道题得30分,其余4道题中有3道题目答对的概率是
,最后1道题目答对的概率是
,从而可求该生选择题得满分的概率;
(2)X的所有可能取值是30,35,40,45,50,求出相应的概率,可得X的分布列与期望,即可得出结论.
| 1 |
| 2 |
| 1 |
| 4 |
(2)X的所有可能取值是30,35,40,45,50,求出相应的概率,可得X的分布列与期望,即可得出结论.
解答:
解:(1)由题意,该学生必可答对前6道题得30分,其余4道题中有3道题目答对的概率是
,最后1道题目答对的概率是
.
记该生选择题得满分为事件M,则P(M)=
•(
)3•
=
.(5分)
(2)X的所有可能取值是30,35,40,45,50.
P(X=30)=
•(
)3•
=
,
P(X=35)=
•
•(
)2•
+
•(
)3•
=
,
P(X=40)=
•(
)2•
•
+
•
•(
)2•
=
,
P(X=45)=
•(
)3•
+
•(
)2•
•
=
,
P(X=50)=
•(
)3•
=
,
所以X的分布列为
故EX=30×
+35×
+40×
+45×
+50×
=38.75.
因为EX=38.75<40,所以该学生还应继续努力以提高正确率.(12分)
| 1 |
| 2 |
| 1 |
| 4 |
记该生选择题得满分为事件M,则P(M)=
| C | 3 3 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 32 |
(2)X的所有可能取值是30,35,40,45,50.
P(X=30)=
| C | 3 3 |
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 32 |
P(X=35)=
| C | 1 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
| C | 3 3 |
| 1 |
| 2 |
| 1 |
| 4 |
| 5 |
| 16 |
P(X=40)=
| C | 2 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
| C | 1 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 8 |
P(X=45)=
| C | 3 3 |
| 1 |
| 2 |
| 3 |
| 4 |
| C | 2 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 16 |
P(X=50)=
| C | 3 3 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 32 |
所以X的分布列为
| X | 30 | 35 | 40 | 45 | 50 | ||||||||||
| P |
|
|
|
|
|
| 3 |
| 32 |
| 5 |
| 16 |
| 3 |
| 8 |
| 3 |
| 16 |
| 1 |
| 32 |
因为EX=38.75<40,所以该学生还应继续努力以提高正确率.(12分)
点评:本题考查概率知识的运用,考查概率的计算,考查随机变量的分布列与期望,考查学生利用数学知识解决实际问题的能力,属于中档题.

练习册系列答案
相关题目
若实数x,y满足不等式组
,则|x+y|的最小值为( )
|
| A、3 | B、-1 | C、1 | D、2 |
下列说法正确的是( )
| A、若已知两个变量具有线性相关关系,且它们正相关,则其线性回归直线的斜率为正 |
| B、直线l垂直于平面α的充要条件为l垂直于平面α内的无数条直线 |
| C、若随机变量ξ~N(10,0.12),且P(9.9<ξ<10.1)=0.6826,则P(ξ>10.1)=0.3174 |
| D、已知命题P:?x∈R,x2-2x+2>0,则¬p:?x∈R,x2-2x+2<0 |
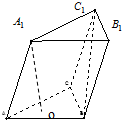 已知三棱柱ABC-A1B1C1的侧棱长和底面边长均为2,A1在底面ABC内的射影O为底面△ABC的中心,如图所示:
已知三棱柱ABC-A1B1C1的侧棱长和底面边长均为2,A1在底面ABC内的射影O为底面△ABC的中心,如图所示: