题目内容
设y=f(x)是二次函数,方程f(x)=0有两个相等的实根,且f′(x)=2x+2.
(Ⅰ)求f(x)的表达式;
(Ⅱ)求由曲线y=f(x)、直线x=-1、直线x=0以及直线y=0围成的曲边梯形面
(Ⅲ)求由曲线段y=f(x)(0≤x≤1)绕x轴旋转一周所得旋转体的体积.
(Ⅰ)求f(x)的表达式;
(Ⅱ)求由曲线y=f(x)、直线x=-1、直线x=0以及直线y=0围成的曲边梯形面
(Ⅲ)求由曲线段y=f(x)(0≤x≤1)绕x轴旋转一周所得旋转体的体积.
考点:二次函数的性质,导数的运算,定积分,定积分的简单应用
专题:函数的性质及应用
分析:(Ⅰ)利用判别式为0,以及函数的导数,求出a、b、c,即可求f(x)的表达式;
(Ⅱ)直接利用定积分求解由曲线y=f(x)、直线x=-1、直线x=0以及直线y=0围成的曲边梯形面
(Ⅲ)通过定积分求由曲线段y=f(x)(0≤x≤1)绕x轴旋转一周所得旋转体的体积.
(Ⅱ)直接利用定积分求解由曲线y=f(x)、直线x=-1、直线x=0以及直线y=0围成的曲边梯形面
(Ⅲ)通过定积分求由曲线段y=f(x)(0≤x≤1)绕x轴旋转一周所得旋转体的体积.
解答:
(本小题满分9分)
解:(I)设f(x)=ax2+bx+c,
∴f′(x)=2ax+b,
又f′(x)=2x+2,∴a=1,b=2,
∴f(x)=x2+2x+c=0,
又方程f(x)=x2+2x+c=0有两个相等的实根,
∴△=0,解得c=1,
∴f(x)=x2+2x+1…(3分)
(II)设由曲线y=f(x)、直线x=-1、直线x=0及直线y=0围成的曲边梯形面积为S,
则S=
(x+)2dx=
(x+1
=
…(6分)
(III)设由曲线段y=f(x)(0≤x≤1)绕x轴旋转一周所得旋转体的体积为V,
则V=π
(x+1)4dx=π×
(x+1)5
=
…(9分).
解:(I)设f(x)=ax2+bx+c,
∴f′(x)=2ax+b,
又f′(x)=2x+2,∴a=1,b=2,
∴f(x)=x2+2x+c=0,
又方程f(x)=x2+2x+c=0有两个相等的实根,
∴△=0,解得c=1,
∴f(x)=x2+2x+1…(3分)
(II)设由曲线y=f(x)、直线x=-1、直线x=0及直线y=0围成的曲边梯形面积为S,
则S=
| ∫ | 0 -1 |
| 1 |
| 3 |
| )3| | 0 -1 |
| 1 |
| 3 |
(III)设由曲线段y=f(x)(0≤x≤1)绕x轴旋转一周所得旋转体的体积为V,
则V=π
| ∫ | 1 0 |
| π |
| 5 |
| | | 1 0 |
| 31π |
| 5 |
点评:本题考查二次函数的基本性质以及定积分的应用,考查分析问题解决问题的能力.

练习册系列答案
相关题目
已知O是锐角△ABC的外心,若
=x
+y
(x,y∈R),则( )
| OC |
| OA |
| OB |
| A、x+y≤-2 |
| B、-2≤x+y<-1 |
| C、x+y<-1 |
| D、-1<x+y<0 |
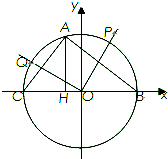 如图,已知B、C是以原点O为圆心,半径为1的圆与x轴的交点,点A在劣弧
如图,已知B、C是以原点O为圆心,半径为1的圆与x轴的交点,点A在劣弧 |
| PQ |
| AH |
| AB |
| AC |
A、(0,
| ||||
B、[
| ||||
C、[
| ||||
D、[
|
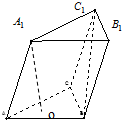 已知三棱柱ABC-A1B1C1的侧棱长和底面边长均为2,A1在底面ABC内的射影O为底面△ABC的中心,如图所示:
已知三棱柱ABC-A1B1C1的侧棱长和底面边长均为2,A1在底面ABC内的射影O为底面△ABC的中心,如图所示: