题目内容
已知平面α内有一个以AB为直径的圆，PA⊥α，点C在圆周上（不同于A、B两点），点D、E分别是点A在PC、PB上的射影，则（ ）
| A、PC⊥面ADE |
| B、∠ACB是二面角A-PC-B的平面角 |
| C、BC∥面ADE |
| D、PB⊥面ADE |
考点：空间中直线与平面之间的位置关系
专题：空间位置关系与距离
分析：利用射影的定义、直径所对的圆周角为直角等知识判定线线垂直，AE⊥PB，AD⊥PC，BC⊥AC．然后利用线线垂直?线面垂直?面面垂直的相互转化关系判定即可．
解答：
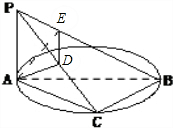解：∵PA⊥⊙O所在平面α，BC?α，
∴PA⊥BC，
∵AB是⊙O的直径，
∴BC⊥AC，
∵PA∩AC=A，
∴BC⊥平面PAC，
∴AD⊥BC，
又∵D是点A在PC上的射影，
∴AD⊥PC，
∵BC∩PC=C，
∴AD⊥平面PBC，
∴AD⊥PB，
又∵AE⊥PB，AD∩AE=A
∴PB⊥面ADE，
故选：D
解：∵PA⊥⊙O所在平面α，BC?α，∴PA⊥BC，
∵AB是⊙O的直径，
∴BC⊥AC，
∵PA∩AC=A，
∴BC⊥平面PAC，
∴AD⊥BC，
又∵D是点A在PC上的射影，
∴AD⊥PC，
∵BC∩PC=C，
∴AD⊥平面PBC，
∴AD⊥PB，
又∵AE⊥PB，AD∩AE=A
∴PB⊥面ADE，
故选：D
点评：本题考查空间中垂直关系的判定，要准确把握线线垂直?线面垂直?面面垂直相互转化的条件．
练习册系列答案
相关题目
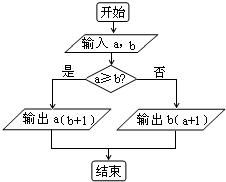
执行如图所示的程序框图，则输出的结果是（ ）
| A、5 | B、7 | C、9 | D、11 |
对于实数a和b，定义运算a*b，运算原理如图所示，则式子(
)-2*lne2的值为（ ）
| 1 |
| 2 |
| A、8 | ||
| B、10 | ||
| C、12 | ||
D、
|