题目内容
19.已知集合M={(x,y)|y=$\sqrt{25-{x}^{2}}$,y≠0},N={(x,y)|y=-x+b},若M∩N≠∅,则实数b的取值范围是( )| A. | (-5,5$\sqrt{2}$] | B. | [-5$\sqrt{2}$,5$\sqrt{2}$] | C. | [-5,5] | D. | [-5$\sqrt{2}$,5) |
分析 由M与N,以及两集合交集不为空集,确定出b的范围即可
解答 解:解:画出M与N中两函数图象,如图所示,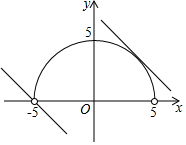
∵M={(x,y)|y=$\sqrt{25-{x}^{2}}$,y≠0},N={(x,y)|y=-x+b},且M∩N≠∅,
∴半圆y=$\sqrt{25-{x}^{2}}$与直线y=-x+b有公共点,
当直线y=-x+b与半圆相切时,圆心(0,0)到直线y=-x+b的距离d=r,即$\frac{|b|}{\sqrt{2}}$=5,
解得:b=5$\sqrt{2}$(负值舍去),
把(-5,0)代入y=-x+b得:b=-5,
则实数b的范围是(-5,5$\sqrt{5}$],
故选:A.
点评 此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
相关题目
9.若复数z满足(1+3i)z=i-3,则z等于( )
| A. | i | B. | $\frac{4-3i}{5}$ | C. | -i | D. | $\frac{5}{2}i$ |
10.若角α的始边是x轴正半轴,终边过点P(4,-3),则cosα的值是( )
| A. | 4 | B. | -3 | C. | $\frac{4}{5}$ | D. | -$\frac{3}{5}$ |
14.在空间中,下列命题正确的是( )
| A. | 如果平面α⊥平面β,任取直线m?α,那么必有m⊥β | |
| B. | 如果直线m∥平面α,直线n?α内,那么m∥n | |
| C. | 如果直线m∥平面α,直线n∥平面α,那么m∥n | |
| D. | 如果平面α外的一条直线m垂直于平面α内的两条相交直线,那么m⊥α |
 如图所示的几何体中,四边形ABCD是菱形,ADNM是矩形,平面ADNM⊥平面ABCD,∠DAB=$\frac{π}{3}$,AD=4,AM=2,E是AB的中点
如图所示的几何体中,四边形ABCD是菱形,ADNM是矩形,平面ADNM⊥平面ABCD,∠DAB=$\frac{π}{3}$,AD=4,AM=2,E是AB的中点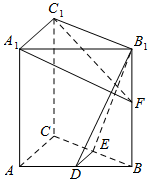 如图,在直三棱柱ABC-A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱B1B上,且B1D⊥A1F,A1C1⊥A1B1.求证:
如图,在直三棱柱ABC-A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱B1B上,且B1D⊥A1F,A1C1⊥A1B1.求证: