题目内容
5.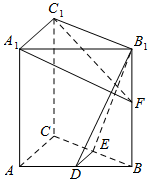 如图,在直三棱柱ABC-A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱B1B上,且B1D⊥A1F,A1C1⊥A1B1.求证:
如图,在直三棱柱ABC-A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱B1B上,且B1D⊥A1F,A1C1⊥A1B1.求证:(1)直线DE∥平面A1C1F;
(2)平面B1DE⊥平面A1C1F.
分析 (1)推导出DE∥AC,从而DE∥A1C1,由此能证明DE∥平面A1C1F.
(2)推导出AA1⊥A1C1,从而A1C1⊥平面AA1B1B,进而DE⊥平面AA1B1B,再由DE⊥A1F,得A1F⊥平面B1DE,由此能证明平面B1DE⊥平面A1C1F.
解答 (本小题满分14分)
证明:(1)∵D,E为中点,
∴DE为△ABC的中位线,∴DE∥AC,
又∵ABC-A1B1C1为棱柱,
∴AC∥A1C1,∴DE∥A1C1,
又∵A1C1?平面A1C1F,且DE?A1C1F,
∴DE∥平面A1C1F.…(6分)
(2)∵ABC-A1B1C1为直棱柱,
∴AA1⊥平面A1B1C1,∴AA1⊥A1C1,
又∵A1C1⊥A1B1且AA1∩A1B1=A1,AA1,A1B1?平面AA1B1B,
∴A1C1⊥平面AA1B1B,
又A1C1∥AC∥DE,∴DE⊥平面AA1B1B,
又∵A1F?平面AA1B1B,∴DE⊥A1F
又∵A1F⊥B1D,DE∩B1D=D,且DE,B1D?平面B1DE,
∴A1F⊥平面B1DE,
又∵A1F?A1C1F,∴平面B1DE⊥平面A1C1F.…(14分)
点评 本题考查线面平行的证明,考查面面垂直的证明,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
19.已知集合M={(x,y)|y=$\sqrt{25-{x}^{2}}$,y≠0},N={(x,y)|y=-x+b},若M∩N≠∅,则实数b的取值范围是( )
| A. | (-5,5$\sqrt{2}$] | B. | [-5$\sqrt{2}$,5$\sqrt{2}$] | C. | [-5,5] | D. | [-5$\sqrt{2}$,5) |
16.化简$\sqrt{1-si{n}^{2}α}$的结果为( )
| A. | sinα | B. | -sinα | C. | ±cosα | D. | -cosα |
13.若椭圆$\frac{x^2}{5}+\frac{y^2}{m}=1$的离心率为$e=\frac{1}{2}$,则m的值为( )
| A. | $\frac{20}{3}$ | B. | $\frac{15}{4}$或$\frac{20}{3}$ | C. | $\frac{15}{4}$ | D. | $\frac{20}{4}$ |
17.函数y=e|-lnx|-|x-1|的图象大致是( )
| A. |  | B. |  | C. |  | D. |  |
14.若f(x)=ex,则$\lim_{△x→0}\frac{{f({1+2△x})-f(1)}}{△x}$=( )
| A. | e | B. | 2e | C. | -e | D. | $\frac{1}{2}e$ |