题目内容
14．在空间中，下列命题正确的是（ ）| A． | 如果平面α⊥平面β，任取直线m?α，那么必有m⊥β | |
| B． | 如果直线m∥平面α，直线n?α内，那么m∥n | |
| C． | 如果直线m∥平面α，直线n∥平面α，那么m∥n | |
| D． | 如果平面α外的一条直线m垂直于平面α内的两条相交直线，那么m⊥α |
分析 A，正方体ABCD-A′B′C′D′，中平面ABCD⊥平面A′ADD′，直线AD′不垂直β；
B，如果直线m∥平面α，直线n?α内，那么m∥n或异面；
C，如果直线m∥平面α，直线n∥平面α，那么m∥n或异面或相交；
对于D，根据线面垂直的判定判定．
解答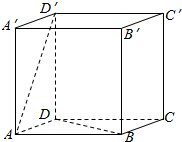 
解：对于A，如图平面ABCD⊥平面A′ADD′，直线AD′不垂直β，故错；
对于B，如果直线m∥平面α，直线n?α内，那么m∥n或异面，故错；
对于C，如果直线m∥平面α，直线n∥平面α，那么m∥n或异面或相交，故错；
对于D，根据线面垂直的判定，如果平面α外的一条直线m垂直于平面α内的两条相交直线，那么m⊥α，正确．
故选：D．
点评 本题考查了空间线线、线面、面面位置关系，属于基础题．
练习册系列答案
相关题目
4．在封闭的直三棱柱ABC-A1B1C1内有一个体积为V的球，若AB⊥BC，AB=6，BC=8，AA1=5，则V的最大值是（ ）
| A． | 4π | B． | $\frac{9π}{2}$ | C． | $\frac{125π}{6}$ | D． | $\frac{32π}{3}$ |
9．设函数$f（x）=\frac{{{e^2}{x^2}+1}}{x}，g（x）=\frac{{{e^2}x}}{e^x}$，对任意x1，x2∈（0，+∞），不等式$\frac{{g（{x_1}）}}{k}≤\frac{{f（{x_2}）}}{k+1}$恒成立，则正数k的取值范围是（ ）
| A． | [1，+∞） | B． | （1，+∞） | C． | $[\frac{1}{2e-1}，+∞）$ | D． | $（\frac{1}{2e-1}，+∞）$ |
19．已知集合M={（x，y）|y=$\sqrt{25-{x}^{2}}$，y≠0}，N={（x，y）|y=-x+b}，若M∩N≠∅，则实数b的取值范围是（ ）
| A． | （-5，5$\sqrt{2}$] | B． | [-5$\sqrt{2}$，5$\sqrt{2}$] | C． | [-5，5] | D． | [-5$\sqrt{2}$，5） |
2．设函数f（x）=x2+bx+c（b，c∈R），若对任意x1，x2∈[-1，1]，有|f（x1）-f（x2）|≤4，则b的取值范围是（ ）
| A． | [0，2] | B． | （0，2] | C． | （-2，2） | D． | [-2，2] |