题目内容
4. 如图所示的几何体中,四边形ABCD是菱形,ADNM是矩形,平面ADNM⊥平面ABCD,∠DAB=$\frac{π}{3}$,AD=4,AM=2,E是AB的中点
如图所示的几何体中,四边形ABCD是菱形,ADNM是矩形,平面ADNM⊥平面ABCD,∠DAB=$\frac{π}{3}$,AD=4,AM=2,E是AB的中点(1)求证:平面MDE⊥平面NDC
(2)求三棱锥N-MDC的体积.
分析 (1)推导出DE⊥CD,ND⊥AD,从而ND⊥DE,进而DE⊥平面NDC,由此能证明平面MAE⊥平面NDC.
(2)由VN-MDC=VM-NDC=VE-NDC,能求出三棱锥N-MDC的体积.
解答 证明:(1)∵ABCD是菱形,∴AD=AB,
∵∠DAB=$\frac{π}{3}$,∴△ABD为等边三角形,
E为AB中点,∴DE⊥AB,∴DE⊥CD,
∵ADMN是矩形,∴ND⊥AD,
又平面ADMN⊥平面ABCD,平面ADMN∩平面ABCD=AD,
∴ND⊥平面ABCD,∴ND⊥DE,
∵CD∩ND=D,∴DE⊥平面NDC,
∵DE?平面MDE,∴平面MAE⊥平面NDC.
解:(2)∵MA∥ND,∴MA∥平面NDC,∴ME∥平面NDC,
∴平面MAE⊥平面NDC,∴ME∥平面NDC,
∴VN-MDC=VM-NDC=VE-NDC,
由(1)知DE⊥AB,∠DAE=$\frac{π}{3}$,
∵DA=4,AE=2,∴DE=2$\sqrt{3}$,
∴三棱锥N-MDC的体积VN-MDC=VM-NDC=VE-NDC=$\frac{1}{3}{S}_{△NDC}•DE$=$\frac{8\sqrt{3}}{3}$.
点评 本题考查面面垂直的证明,考查三棱锥的体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
15.设实数x1、x2是函数$f(x)=|{lnx}|-{({\frac{1}{2}})^x}$的两个零点,则( )
| A. | x1x2<0 | B. | 0<x1x2<1 | C. | x1x2=1 | D. | x1x2>1 |
12.若f(x)=xsinx,则函数f(x)的导函数f′(x)等于( )
| A. | 1-sinx | B. | x-sinx | C. | sinx+xcosx | D. | cosx-xsinx |
19.已知集合M={(x,y)|y=$\sqrt{25-{x}^{2}}$,y≠0},N={(x,y)|y=-x+b},若M∩N≠∅,则实数b的取值范围是( )
| A. | (-5,5$\sqrt{2}$] | B. | [-5$\sqrt{2}$,5$\sqrt{2}$] | C. | [-5,5] | D. | [-5$\sqrt{2}$,5) |
9.函数y=-lg(x+1)的图象是( )
| A. |  | B. |  | C. |  | D. |  |
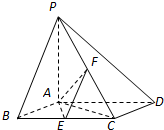 如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.
如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.