题目内容
7.已知函数f(x)=$\frac{1}{2}$x2-ax+blnx+4在x=1处取得极值$\frac{3}{2}$,则实数a+b=5.分析 求出函数的导数,得到关于a,b的方程,求出a,b的值,从而求出a+b的值即可.
解答 解:f(x)=$\frac{1}{2}$x2-ax+blnx+4,(x>0),
f′(x)=x-a+$\frac{b}{x}$,
若函数f(x)在x=1处取得极值$\frac{3}{2}$,
则f′(1)=1-a+b=0①,
f(1)=$\frac{1}{2}$-a+4=$\frac{3}{2}$②,
由①②解得:a=3,b=2,
故a+b=5,
故答案为:5.
点评 本题考查了函数的单调性、极值问题,考查导数的应用,是一道中档题.

练习册系列答案
相关题目
19.已知集合M={(x,y)|y=$\sqrt{25-{x}^{2}}$,y≠0},N={(x,y)|y=-x+b},若M∩N≠∅,则实数b的取值范围是( )
| A. | (-5,5$\sqrt{2}$] | B. | [-5$\sqrt{2}$,5$\sqrt{2}$] | C. | [-5,5] | D. | [-5$\sqrt{2}$,5) |
2.设函数f(x)=x2+bx+c(b,c∈R),若对任意x1,x2∈[-1,1],有|f(x1)-f(x2)|≤4,则b的取值范围是( )
| A. | [0,2] | B. | (0,2] | C. | (-2,2) | D. | [-2,2] |
16.化简$\sqrt{1-si{n}^{2}α}$的结果为( )
| A. | sinα | B. | -sinα | C. | ±cosα | D. | -cosα |
17.函数y=e|-lnx|-|x-1|的图象大致是( )
| A. |  | B. |  | C. |  | D. |  |
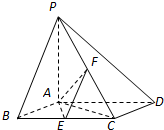 如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.
如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.