题目内容
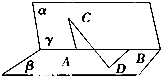如图，120°的二面角的棱上有A，B两点，AC，BD分别是在这个二面角的两个半平面内垂直于AB的线段，且AB=4cm，AC=6cm，BD=8cm，则CD的长为考点：点、线、面间的距离计算
专题：空间位置关系与距离
分析：由已知可得
=
+
+
，
•
=0，
•
=0，利用数量积的性质即可得出．
| CD |
| CA |
| AB |
| BD |
| CA |
| AB |
| AB |
| BD |
解答：
解：由条件，知
•
=0，
•
=0．
所以|
|2=|
|2+|
|2+|
|2+2
•
+2
•
+2
•
=62+42+82+2×6×8cos60°=164，
所以CD=2
cm，
故答案为：2
cm．
| CA |
| AB |
| AB |
| BD |
所以|
| CD |
| CA |
| AB |
| BD |
| CA |
| AB |
| AB |
| BD |
| CA |
| BD |
=62+42+82+2×6×8cos60°=164，
所以CD=2
| 41 |
故答案为：2
| 41 |
点评：本题考查面面角，考查空间距离的计算，熟练掌握向量的运算和数量积运算是解题的关键．
练习册系列答案
相关题目
已知命题p：?x1，x2∈R，[f（x2）-f（x1）]（x1-x2）≥0，则￢p是（ ）
| A、?x1，x2∈R，[f（x2）-f（x1）]（x1-x2）≤0 |
| B、?x1，x2∈R，[f（x2）-f（x1）]（x1-x2）≤0 |
| C、?x1，x2∈R，[f（x2）-f（x1）]（x1-x2）π≥0 |
| D、?x1，x2∈R，[f（x2）-f（x1）]（x1-x2）π≥0 |
设α是空间中的一个平面，l，m，n是三条不同的直线，则下列命题中正确的是（ ）
| A、若m?α，n?α，l⊥m，l⊥n，则l⊥α |
| B、若m?α，n⊥α，l⊥n，则l∥m |
| C、若l⊥m，l⊥n，则n∥m |
| D、若m⊥α，n⊥α，则n∥m |