题目内容
设α是空间中的一个平面,l,m,n是三条不同的直线,则下列命题中正确的是( )
| A、若m?α,n?α,l⊥m,l⊥n,则l⊥α |
| B、若m?α,n⊥α,l⊥n,则l∥m |
| C、若l⊥m,l⊥n,则n∥m |
| D、若m⊥α,n⊥α,则n∥m |
考点:空间中直线与平面之间的位置关系,平面与平面之间的位置关系
专题:常规题型,空间位置关系与距离
分析:在正方体中找反例,对四个选项一一验证即可.
解答:
 解:如图:
解:如图:
在正方体中,A1C1⊥B1D1,A1C1⊥EF,但A1C1?平面B1D1A1C1,故A错误;
在正方体中,A1C1?平面B1D1A1C1,AA1⊥平面B1D1A1C1,AA1⊥AB,AB与A1C1不平行,故错误;
在正方体中取共点的三条棱即可,故C不正确;
故选D.
 解:如图:
解:如图:在正方体中,A1C1⊥B1D1,A1C1⊥EF,但A1C1?平面B1D1A1C1,故A错误;
在正方体中,A1C1?平面B1D1A1C1,AA1⊥平面B1D1A1C1,AA1⊥AB,AB与A1C1不平行,故错误;
在正方体中取共点的三条棱即可,故C不正确;
故选D.
点评:本题考查了线面的位置关系,同学们要习惯应用正方体中的线面举反例,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在△ABC中,a2=b2+c2-bc,则A的值为( )
| A、30° |
| B、60° |
| C、30°或150° |
| D、60°或120° |
已知命题p:“?x∈R,|x|+x2>0“,命题q:“a+c>b+d“是a>b且c>d的充分不必要条件”,则下列结论正确的是( )
| A、命题“p∧q”是真命题 |
| B、命题“(¬p)∧q”是真命题 |
| C、命题“p∧(-q)”是真命题 |
| D、命题“p∨q”是假命题 |
已知数列{an}是递增等差数列,若a2014+a2015<0,a2014•a2015<0,且数列{an}的前n项和Sn有最小值,那么Sn取得最小正值时n等于( )
| A、4029 | B、4028 |
| C、4027 | D、4026 |
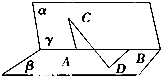 如图,120°的二面角的棱上有A,B两点,AC,BD分别是在这个二面角的两个半平面内垂直于AB的线段,且AB=4cm,AC=6cm,BD=8cm,则CD的长为
如图,120°的二面角的棱上有A,B两点,AC,BD分别是在这个二面角的两个半平面内垂直于AB的线段,且AB=4cm,AC=6cm,BD=8cm,则CD的长为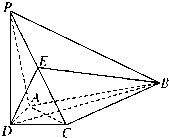 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD=CD,DB平分∠ADC,E为PC的中点.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD=CD,DB平分∠ADC,E为PC的中点.