题目内容
已知数列{an}是公差不为零的等差数列,且a2=3,又a4,a5,a8成等比数列.
(1)求数列{an}的通项公式;
(2)求Sn及使得Sn最大的序号n的值.
(1)求数列{an}的通项公式;
(2)求Sn及使得Sn最大的序号n的值.
考点:数列与不等式的综合
专题:等差数列与等比数列
分析:(1)设出等数数列的首项、公差,然后结合已知条件列出方程组解之即可;
(2)将Sn表示出来,是一个关于n的二次函数,然后利用配方法求其最大值,注意n是N*.
(2)将Sn表示出来,是一个关于n的二次函数,然后利用配方法求其最大值,注意n是N*.
解答:
解:(1)因为a4,a5,a8成等比数列,所以a52=a4a8.
设等差数列{an}的公差为d,则(a2+3d)2=(a2+2d)(a2+6d),
因为a2=3,所以d2+2d=0.
又因为d≠0,所以d=-2.
所以an=-2n+7.
(2)由(1)知,a1=5,d=-2.
所以Sn=na1+
d=6n-n2.
因为Sn=-(n-3)2+9.(n∈N*)
故当n=3时,Sn取得最大值9.
故所求的和Sn的最大值为9.
设等差数列{an}的公差为d,则(a2+3d)2=(a2+2d)(a2+6d),
因为a2=3,所以d2+2d=0.
又因为d≠0,所以d=-2.
所以an=-2n+7.
(2)由(1)知,a1=5,d=-2.
所以Sn=na1+
| n(n-1) |
| 2 |
因为Sn=-(n-3)2+9.(n∈N*)
故当n=3时,Sn取得最大值9.
故所求的和Sn的最大值为9.
点评:(1)突出基本量的思想,即用首项、公差表示出题目已给的条件,列方程(组)求解;
(2)将前n项和表示成n的函数,利用函数的性质(单调性等,或配方法)求其最值,注意n的取值为正整数.
(2)将前n项和表示成n的函数,利用函数的性质(单调性等,或配方法)求其最值,注意n的取值为正整数.

练习册系列答案
相关题目
圆C1的方程为x2+y2=
,圆C2的方程(x-cosθ)2+(y-sinθ)2=
(θ∈R),过C2上任意一点P作圆C1的两条切线PM、PN,切点分别为M、N,则∠MPN的最大值为( )
| 4 |
| 25 |
| 1 |
| 25 |
A、
| ||
B、
| ||
C、
| ||
D、
|
集合P={(x,y)|(x-2cosθ)2+(y-2sinθ)2=1,0≤θ≤2π},集合Q={(x,y)|y≥
x},若P⊆Q,则θ的取值范围是( )
| ||
| 3 |
A、[
| ||||
B、[
| ||||
C、[
| ||||
D、[
|
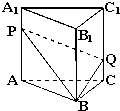 如图,已知直三棱柱ABC-A1B1C1,点P、Q分别在棱AA1和CC1上,AP=C1Q,则平面BPQ把三棱柱分成两部分的体积比为( )
如图,已知直三棱柱ABC-A1B1C1,点P、Q分别在棱AA1和CC1上,AP=C1Q,则平面BPQ把三棱柱分成两部分的体积比为( )| A、2:1 | B、3:1 |
| C、3:2 | D、4:3 |
已知直线ax+2y+2=0与直线3x-y-2=0平行,则a的值为( )
| A、-6 | B、6 | C、-3 | D、3 |




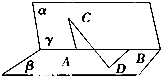 如图,120°的二面角的棱上有A,B两点,AC,BD分别是在这个二面角的两个半平面内垂直于AB的线段,且AB=4cm,AC=6cm,BD=8cm,则CD的长为
如图,120°的二面角的棱上有A,B两点,AC,BD分别是在这个二面角的两个半平面内垂直于AB的线段,且AB=4cm,AC=6cm,BD=8cm,则CD的长为