题目内容
数列{an}是递增的等差数列,且a1+a6=-6,a3•a4=8.
(1)求数列{an}的通项公式;
(2)求数列{|an|}的前n项和Tn.
(1)求数列{an}的通项公式;
(2)求数列{|an|}的前n项和Tn.
考点:数列的求和
专题:等差数列与等比数列
分析:(1)设递增的等差数列{an}的公差d>0,由于a1+a6=-6,a3•a4=8.可得
,解出即可.
(2))设Sn=a1+a2+…+an,可得Sn=n2-9n.由an≤0,解得n≤5.当n≤5时,Tn=-a1-a2-…-an=-Sn.当n≥6时,Tn=-2S5-Sn.
|
(2))设Sn=a1+a2+…+an,可得Sn=n2-9n.由an≤0,解得n≤5.当n≤5时,Tn=-a1-a2-…-an=-Sn.当n≥6时,Tn=-2S5-Sn.
解答:
解:(1)设递增的等差数列{an}的公差d>0,
∵a1+a6=-6,a3•a4=8.∴
,
解得
.
∴an=-8+2(n-1)=2n-10.
(2)设Sn=a1+a2+…+an,则Sn=
=n2-9n.
由an≤0,解得n≤5.
∴当n≤5时,Tn=-a1-a2-…-an=-Sn=9n-n2.
当n≥6时,Tn=-a1-a2-…-a5+a6+a7+…+an=-2S5-Sn=40+9n-n2.
∵a1+a6=-6,a3•a4=8.∴
|
解得
|
∴an=-8+2(n-1)=2n-10.
(2)设Sn=a1+a2+…+an,则Sn=
| n(2n-10-8) |
| 2 |
由an≤0,解得n≤5.
∴当n≤5时,Tn=-a1-a2-…-an=-Sn=9n-n2.
当n≥6时,Tn=-a1-a2-…-a5+a6+a7+…+an=-2S5-Sn=40+9n-n2.
点评:本题考查了等差数列的通项公式与前n项和公式、含绝对值符号的数列求和,考查了分类讨论的思想方法,考查了推理能力与计算能力,属于难题.

练习册系列答案
 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
圆C1的方程为x2+y2=
,圆C2的方程(x-cosθ)2+(y-sinθ)2=
(θ∈R),过C2上任意一点P作圆C1的两条切线PM、PN,切点分别为M、N,则∠MPN的最大值为( )
| 4 |
| 25 |
| 1 |
| 25 |
A、
| ||
B、
| ||
C、
| ||
D、
|
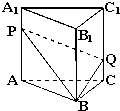 如图,已知直三棱柱ABC-A1B1C1,点P、Q分别在棱AA1和CC1上,AP=C1Q,则平面BPQ把三棱柱分成两部分的体积比为( )
如图,已知直三棱柱ABC-A1B1C1,点P、Q分别在棱AA1和CC1上,AP=C1Q,则平面BPQ把三棱柱分成两部分的体积比为( )| A、2:1 | B、3:1 |
| C、3:2 | D、4:3 |
已知直线ax+2y+2=0与直线3x-y-2=0平行,则a的值为( )
| A、-6 | B、6 | C、-3 | D、3 |
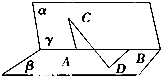 如图,120°的二面角的棱上有A,B两点,AC,BD分别是在这个二面角的两个半平面内垂直于AB的线段,且AB=4cm,AC=6cm,BD=8cm,则CD的长为
如图,120°的二面角的棱上有A,B两点,AC,BD分别是在这个二面角的两个半平面内垂直于AB的线段,且AB=4cm,AC=6cm,BD=8cm,则CD的长为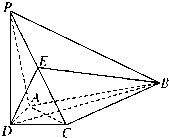 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD=CD,DB平分∠ADC,E为PC的中点.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD=CD,DB平分∠ADC,E为PC的中点.