题目内容
已知圆C:(x-1)2+(y-2)2=25,直线l:(2m+1)x+(m+1)y-7m-4=0(m∈R).
(Ⅰ)求证:无论m取什么实数,直线l都过定点,并写出这个定点的坐标;
(Ⅱ)求直线l被圆C截得的弦长最短时l的方程.
(Ⅰ)求证:无论m取什么实数,直线l都过定点,并写出这个定点的坐标;
(Ⅱ)求直线l被圆C截得的弦长最短时l的方程.
考点:直线和圆的方程的应用
专题:直线与圆
分析:(1)先将直线方程整理成f1(x)+λf2(x)=0的形式,然后通过解方程即可求出其交点.
(2)易知,当定点与圆心连线垂直于该直线时,弦长最短,据此求出直线l的方程.
(2)易知,当定点与圆心连线垂直于该直线时,弦长最短,据此求出直线l的方程.
解答:
解:(Ⅰ)证明:∵直线l的方程等价于(2x+y-7)m+x+y-4=0(1).
令2x+y-7=0,则由x+y-4=0
∴
,解得
,
∴点(3,1)的坐标使方程(1)恒成立.
∴无论m取什么实数,直线l都过定点,定点的坐标为(3,1).
(Ⅱ)解:由(Ⅰ)知,直线恒过定点P(3,1).

当x=3,y=1时,(x-1)2+(y-2)2=(3-1)2+(1-2)2<25
∴点P在圆C内.由图知,r2-d2=(
)2.r是定值5.
∴当d取最大值时,AB最短.
又l⊥CP时,d取最大值.此时kCP=-
,kl=2.
∴l的方程为y-1=2(x-3),即2x-y-5=0.
令2x+y-7=0,则由x+y-4=0
∴
|
|
∴点(3,1)的坐标使方程(1)恒成立.
∴无论m取什么实数,直线l都过定点,定点的坐标为(3,1).
(Ⅱ)解:由(Ⅰ)知,直线恒过定点P(3,1).

当x=3,y=1时,(x-1)2+(y-2)2=(3-1)2+(1-2)2<25
∴点P在圆C内.由图知,r2-d2=(
| AB |
| 2 |
∴当d取最大值时,AB最短.
又l⊥CP时,d取最大值.此时kCP=-
| 1 |
| 2 |
∴l的方程为y-1=2(x-3),即2x-y-5=0.
点评:本题考查了交点直线系方程的特点及其应用,同时研究了直线与圆的相交弦问题,此类问题一般是结合垂径定理进行研究,即半径、弦心距、二分之一弦长符合勾股定理.由此进一步进行分析.

练习册系列答案
相关题目
已知命题p:“?x∈R,|x|+x2>0“,命题q:“a+c>b+d“是a>b且c>d的充分不必要条件”,则下列结论正确的是( )
| A、命题“p∧q”是真命题 |
| B、命题“(¬p)∧q”是真命题 |
| C、命题“p∧(-q)”是真命题 |
| D、命题“p∨q”是假命题 |
已知数列{an}是递增等差数列,若a2014+a2015<0,a2014•a2015<0,且数列{an}的前n项和Sn有最小值,那么Sn取得最小正值时n等于( )
| A、4029 | B、4028 |
| C、4027 | D、4026 |
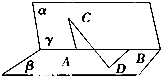 如图,120°的二面角的棱上有A,B两点,AC,BD分别是在这个二面角的两个半平面内垂直于AB的线段,且AB=4cm,AC=6cm,BD=8cm,则CD的长为
如图,120°的二面角的棱上有A,B两点,AC,BD分别是在这个二面角的两个半平面内垂直于AB的线段,且AB=4cm,AC=6cm,BD=8cm,则CD的长为