题目内容
已知函数f(x)=(
)x的图象与函y=g(x)的图象关于直线y=x对称,令h(x)=g(1-x2),则关于h(x)有下列命题:
①h(x)的图象关于原点对称;
②h(x)为偶函数;
③h(x)的最小值为0;
④h(x)在(0,1)上为增函数.
其中正确命题的序号为 .(将你认为正确的命题的序号都填上)
| 1 |
| 2 |
①h(x)的图象关于原点对称;
②h(x)为偶函数;
③h(x)的最小值为0;
④h(x)在(0,1)上为增函数.
其中正确命题的序号为
考点:指数函数的图像与性质,对数函数的图像与性质
专题:函数的性质及应用
分析:先根据函数f(x)=(
)x的图象与函数g(x)的图象关于直线y=x对称,求出函数g(x)的解析式,然后根据奇偶性的定义进行判定,根据复合函数的单调性进行判定可求出函数的最值,从而得到正确选项.
| 1 |
| 2 |
解答:
解:∵函数f(x)=(
)x的图象与函数g(x)的图象关于直线y=x对称,
∴g(x)=log
(1-x2)
∵h(x)=g(1-x2)=log
(1-x2),x∈(-1,1)
而h(-x)=log
(1-x2)=h(x)
则h(x)是偶函数,故①不正确,②正确
该函数在(-1,0)上单调递减,在(0,1)上单调递增
∴h(x)有最小值为0,无最大值
故选项③④正确,
故答案为:②③④
| 1 |
| 2 |
∴g(x)=log
| 1 |
| 2 |
∵h(x)=g(1-x2)=log
| 1 |
| 2 |
而h(-x)=log
| 1 |
| 2 |
则h(x)是偶函数,故①不正确,②正确
该函数在(-1,0)上单调递减,在(0,1)上单调递增
∴h(x)有最小值为0,无最大值
故选项③④正确,
故答案为:②③④
点评:本题主要考查了反函数,以及函数的奇偶性、单调性和最值,同时考查了奇偶函数图象的对称性,属于中档题.

练习册系列答案
相关题目
已知数列{an}是递增等差数列,若a2014+a2015<0,a2014•a2015<0,且数列{an}的前n项和Sn有最小值,那么Sn取得最小正值时n等于( )
| A、4029 | B、4028 |
| C、4027 | D、4026 |
已知数列{an}满足an=
(k∈N*),设f(n)=a1+a2+a3+…+a2n-1+a2n,则f(2014)-f(2013)=( )
|
| A、42012 |
| B、42013 |
| C、42014 |
| D、42015 |
若圆C1:x2+y2-2x=0与直线l:y-mx-m=0有两个不同的交点,则实数m的取值范围是( )
A、(-
| ||||||||
B、(-
| ||||||||
C、[-
| ||||||||
D、(-∞,-
|
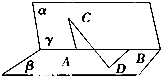 如图,120°的二面角的棱上有A,B两点,AC,BD分别是在这个二面角的两个半平面内垂直于AB的线段,且AB=4cm,AC=6cm,BD=8cm,则CD的长为
如图,120°的二面角的棱上有A,B两点,AC,BD分别是在这个二面角的两个半平面内垂直于AB的线段,且AB=4cm,AC=6cm,BD=8cm,则CD的长为