题目内容
已知动点M到A(0,1)的距离比它到x轴的距离多一个单位.
(Ⅰ)求动点M的轨迹C的方程;
(Ⅱ)过点N(2,1)作曲线C的切线l,求切线l的方程,并求出l与曲线C及y轴所围成图形的面积S.
(Ⅰ)求动点M的轨迹C的方程;
(Ⅱ)过点N(2,1)作曲线C的切线l,求切线l的方程,并求出l与曲线C及y轴所围成图形的面积S.
考点:轨迹方程,利用导数研究曲线上某点切线方程
专题:圆锥曲线的定义、性质与方程
分析:(Ⅰ)直接由题意得到动点M的轨迹为抛物线,由抛物线定义求动点M的轨迹C的方程;
(Ⅱ)利用导数求出曲线C的切线l的方程,然后用定积分求l与曲线C及y轴所围成图形的面积.
(Ⅱ)利用导数求出曲线C的切线l的方程,然后用定积分求l与曲线C及y轴所围成图形的面积.
解答:
解:(Ⅰ)设动点M的坐标为(x,y),
依题意得:动点M到点A的距离与它到直线y=-1的距离相等,
由抛物线定义知:M的轨迹C是以A为焦点,直线y=-1为准线的抛物线,
其方程为:x2=4y;
(Ⅱ)∵曲线C的方程可写成:y=
x2,
注意到点N(2,1)在曲线C上,过点N的切线l斜率为y′|x=2=
x|x=2=1,
故所求的切线l的方程为:y-1=x-2,即y=x-1.
由定积分的几何意义,所求的图形的面积
S
(
x2-x+1)dx=(
x3-
x2+x)
=
.
依题意得:动点M到点A的距离与它到直线y=-1的距离相等,
由抛物线定义知:M的轨迹C是以A为焦点,直线y=-1为准线的抛物线,
其方程为:x2=4y;
(Ⅱ)∵曲线C的方程可写成:y=
| 1 |
| 4 |
注意到点N(2,1)在曲线C上,过点N的切线l斜率为y′|x=2=
| 1 |
| 2 |
故所求的切线l的方程为:y-1=x-2,即y=x-1.
由定积分的几何意义,所求的图形的面积
S
| =∫ | 2 0 |
| 1 |
| 4 |
| 1 |
| 12 |
| 1 |
| 2 |
| | | 2 0 |
| 2 |
| 3 |
点评:本题考查了抛物线的定义及标准方程,考查了利用定积分求曲边梯形的面积,是中档题.

练习册系列答案
相关题目
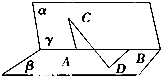 如图,120°的二面角的棱上有A,B两点,AC,BD分别是在这个二面角的两个半平面内垂直于AB的线段,且AB=4cm,AC=6cm,BD=8cm,则CD的长为
如图,120°的二面角的棱上有A,B两点,AC,BD分别是在这个二面角的两个半平面内垂直于AB的线段,且AB=4cm,AC=6cm,BD=8cm,则CD的长为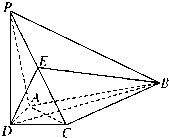 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD=CD,DB平分∠ADC,E为PC的中点.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD=CD,DB平分∠ADC,E为PC的中点.