题目内容
已知命题p：?x1，x2∈R，[f（x2）-f（x1）]（x1-x2）≥0，则￢p是（ ）
| A、?x1，x2∈R，[f（x2）-f（x1）]（x1-x2）≤0 |
| B、?x1，x2∈R，[f（x2）-f（x1）]（x1-x2）≤0 |
| C、?x1，x2∈R，[f（x2）-f（x1）]（x1-x2）π≥0 |
| D、?x1，x2∈R，[f（x2）-f（x1）]（x1-x2）π≥0 |
考点：命题的否定
专题：简易逻辑
分析：直接利用全称命题的否定是特称命题写出结果即可．
解答：
解：因为全称命题的否定是特称命题，
所以命题p：?x1，x2∈R，[f（x2）-f（x1）]（x1-x2）≥0，则￢p是：?x1，x2∈R，[f（x2）-f（x1）]（x1-x2）π≥0；
故选：C．
所以命题p：?x1，x2∈R，[f（x2）-f（x1）]（x1-x2）≥0，则￢p是：?x1，x2∈R，[f（x2）-f（x1）]（x1-x2）π≥0；
故选：C．
点评：本题考查命题的否定特称命题与全称命题的关系，基本知识的考查．
练习册系列答案
浙江名校名师金卷系列答案
相关题目
在△ABC中，a2=b2+c2-bc，则A的值为（ ）
| A、30° |
| B、60° |
| C、30°或150° |
| D、60°或120° |
已知命题p：“?x∈R，|x|+x2＞0“，命题q：“a+c＞b+d“是a＞b且c＞d的充分不必要条件”，则下列结论正确的是（ ）
| A、命题“p∧q”是真命题 |
| B、命题“（￢p）∧q”是真命题 |
| C、命题“p∧（-q）”是真命题 |
| D、命题“p∨q”是假命题 |
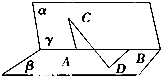如图，120°的二面角的棱上有A，B两点，AC，BD分别是在这个二面角的两个半平面内垂直于AB的线段，且AB=4cm，AC=6cm，BD=8cm，则CD的长为