题目内容
已知三棱锥S-ABC是三条侧棱两两垂直的三棱锥,O是底面△ABC内的一点,则G=tan∠OSA•tan∠OSB•tan∠OSC的最小值是 .
考点:棱锥的结构特征
专题:空间位置关系与距离
分析:过O分别作与SA、SB、SC平行的平面交三棱锥的侧棱,侧面于各点,补形得到以SO为对角线的长方体,利用长方体体对角线的平方等于过一个顶点的三条棱的平方和得到cos2α+cos2β+cos2γ=1,移向变形得到sin2α=1-cos2α=cos2β+cos2γ≥2cosβcosγ及另外类似的两个式子,作积后整理即可得到答案.
解答:
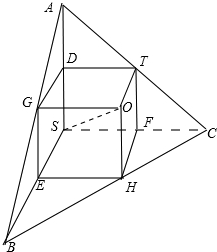 解:如图,设∠OSA=α,∠OSB=β,∠OSC=γ
解:如图,设∠OSA=α,∠OSB=β,∠OSC=γ
过O分别作与SA、SB、SC平行的平面交三棱锥的侧棱,侧面于如图所示的点,
得到的图形是以SO为对角线的长方体,
则cos2α+cos2β+cos2γ=
.
所以sin2α=1-cos2α=cos2β+cos2γ≥2cosβcosγ.
同理sin2β≥2cosαcosγ,sin2γ≥2cosαcosβ.
则sin2α•sin2β•sin2γ≥8cos2α•cos2β•cos2γ.
所以G=tan∠OSA•tan∠OSB•tan∠OSC≥2
,
故答案为2
.
 解:如图,设∠OSA=α,∠OSB=β,∠OSC=γ
解:如图,设∠OSA=α,∠OSB=β,∠OSC=γ过O分别作与SA、SB、SC平行的平面交三棱锥的侧棱,侧面于如图所示的点,
得到的图形是以SO为对角线的长方体,
则cos2α+cos2β+cos2γ=
| SD2 |
| SO2 |
所以sin2α=1-cos2α=cos2β+cos2γ≥2cosβcosγ.
同理sin2β≥2cosαcosγ,sin2γ≥2cosαcosβ.
则sin2α•sin2β•sin2γ≥8cos2α•cos2β•cos2γ.
所以G=tan∠OSA•tan∠OSB•tan∠OSC≥2
| 2 |
故答案为2
| 2 |
点评:本题考查了棱锥的结构特征,考查了同角三角函数的基本关系式,解答的关键是想到补形,把零散的角集中到一个长方体中解决,此题属中档题.

练习册系列答案
相关题目
已知命题p:“?x∈R,|x|+x2>0“,命题q:“a+c>b+d“是a>b且c>d的充分不必要条件”,则下列结论正确的是( )
| A、命题“p∧q”是真命题 |
| B、命题“(¬p)∧q”是真命题 |
| C、命题“p∧(-q)”是真命题 |
| D、命题“p∨q”是假命题 |
已知直线ax+2y+2=0与直线3x-y-2=0平行,则a的值为( )
| A、-6 | B、6 | C、-3 | D、3 |
若圆C1:x2+y2-2x=0与直线l:y-mx-m=0有两个不同的交点,则实数m的取值范围是( )
A、(-
| ||||||||
B、(-
| ||||||||
C、[-
| ||||||||
D、(-∞,-
|
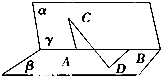 如图,120°的二面角的棱上有A,B两点,AC,BD分别是在这个二面角的两个半平面内垂直于AB的线段,且AB=4cm,AC=6cm,BD=8cm,则CD的长为
如图,120°的二面角的棱上有A,B两点,AC,BD分别是在这个二面角的两个半平面内垂直于AB的线段,且AB=4cm,AC=6cm,BD=8cm,则CD的长为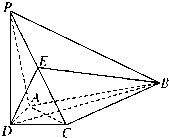 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD=CD,DB平分∠ADC,E为PC的中点.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD=CD,DB平分∠ADC,E为PC的中点.