题目内容
设两个非零向量
和
不共线．
（1）如果
=
-
，
=3
+2
，
=-8
-2
，求证：A、C、D三点共线；
（2）如果
=
+
，
=2
-3
，
=3
-k
，且A、C、F三点共线，求k的值．
| e1 |
| e2 |
（1）如果
| AB |
| e1 |
| e2 |
| BC |
| e1 |
| e2 |
| CD |
| e1 |
| e2 |
（2）如果
| AB |
| e1 |
| e2 |
| BC |
| e1 |
| e2 |
| AF |
| e1 |
| e2 |
考点：平行向量与共线向量
专题：平面向量及应用
分析：（1）利用向量共线定理即可证明；
（2）由于
=
+
=3
-2
，A、C、F三点共线，可得存在实数λ使得
=λ
，利用向量基本定理即可得出．
（2）由于
| AC |
| AB |
| BC |
| e1 |
| e2 |
| AF |
| AC |
解答：
（1）证明：∵
=
+
=4
+
=-
(-8
-2
)=-
，
∴A、C、D三点共线；
（2）∵
=
+
=3
-2
，A、C、F三点共线，
∴存在实数λ使得
=λ
，
∴3
-k
=λ（3
-2
）=3λ
-2λ
，
∵两个非零向量
和
不共线．
∴
，解得k=2．
| AC |
| AB |
| BC |
| e1 |
| e2 |
| 1 |
| 2 |
| e1 |
| e2 |
| 1 |
| 2 |
| CD |
∴A、C、D三点共线；
（2）∵
| AC |
| AB |
| BC |
| e1 |
| e2 |
∴存在实数λ使得
| AF |
| AC |
∴3
| e1 |
| e2 |
| e1 |
| e2 |
| e1 |
| e2 |
∵两个非零向量
| e1 |
| e2 |
∴
|
点评：本题考查了向量共线定理、向量基本定理，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
椭圆
+
=1上有n个不同的点P1、P2、…、Pn，椭圆的右焦点为F，数列{|PnF|}是公差大于
的等差数列，则n的最大值是（ ）
| x2 |
| 4 |
| y3 |
| 3 |
| 1 |
| 1000 |
| A、2 000 |
| B、2 006 |
| C、2 007 |
| D、2 008 |
已知平面内一点P及△ABC，若
+
+
=
，则点P与△ABC的位置关系是（ ）
| PA |
| PB |
| PC |
| AB |
| A、点P在线段AB上 |
| B、点P在线段BC上 |
| C、点P在线段AC上 |
| D、点p在△ABC外部 |
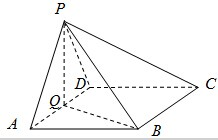在四棱锥P-ABCD中，底面ABCD为菱形，∠BAD=60°，Q为AD的中点，若PA=PD．