题目内容
设x1,x2分别是方程xax=1和xlogax=1的根(其中a>1),则x1+2x2的取值范围( )
A、(2
| ||
B、[2
| ||
| C、(3,+∞) | ||
| D、[3,+∞) |
考点:根的存在性及根的个数判断
专题:计算题,函数的性质及应用
分析:由题意可得ax1=
,a
=x2,从而可得
=x2,x2>1;再由函数的单调性求解.
| 1 |
| x1 |
| 1 |
| x2 |
| 1 |
| x1 |
解答:
解:由题意可得,
x1ax1=1,x2logax2=1;
故ax1=
,a
=x2,
又∵y=ax在(0,+∞)上单调递增,
故
=x2,x2>1;
故x1+2x2=
+2x2,
而y=
+2x2在(1,+∞) 上是增函数,
故
+2x2>3;
故选C.
x1ax1=1,x2logax2=1;
故ax1=
| 1 |
| x1 |
| 1 |
| x2 |
又∵y=ax在(0,+∞)上单调递增,
故
| 1 |
| x1 |
故x1+2x2=
| 1 |
| x2 |
而y=
| 1 |
| x2 |
故
| 1 |
| x2 |
故选C.
点评:本题考查了方程的根的确定及函数的性质的应用,属于中档题.

练习册系列答案
相关题目
某几何体的三视图如图所示,则该几何体的体积为( )
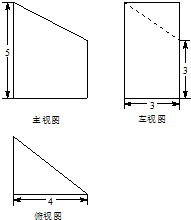

| A、26 | ||
B、42+3
| ||
| C、62 | ||
D、42-3
|