题目内容
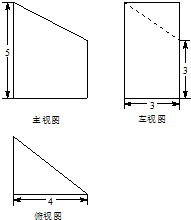
某几何体的三视图如图所示，则该几何体的体积为（ ）
| A、26 | ||
B、42+3
| ||
| C、62 | ||
D、42-3
|
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：由已知中的三视图可得：该几何体是一个三棱柱截去一个三棱锥所得的组合体，分别求出棱柱和棱锥的体积，相减可得答案．
解答：
解：由已知中的三视图可得：该几何体是一个三棱柱截去一个三棱锥所得的组合体，
它们的底面面积S=
×3×4=6，
棱柱的高为5，故体积为：30，
棱锥的高为5-3=2，故体积为：4，
故组合体的体积V=30-4=26，
故选：A
它们的底面面积S=
| 1 |
| 2 |
棱柱的高为5，故体积为：30，
棱锥的高为5-3=2，故体积为：4，
故组合体的体积V=30-4=26，
故选：A
点评：解决三视图的题目，关键是由三视图判断出几何体的形状及度量长度，然后利用几何体的面积及体积公式解决．
练习册系列答案
相关题目
如图在程序框图中，若输入n=6，则输出k的值是（ ）
| A、2 | B、3 | C、4 | D、5 |
设x1，x2分别是方程xax=1和xlogax=1的根（其中a＞1），则x1+2x2的取值范围（ ）
A、（2
| ||
B、[2
| ||
| C、（3，+∞） | ||
| D、[3，+∞） |
已知集合A={x|x2-2x≥0}，B={x|x＜1}，则A∩B=（ ）
| A、[-1，1） |
| B、（0.1） |
| C、[0，1） |
| D、（-∞，0] |
已知A，B是圆O：x2+y2=1上的两个动点，P是AB线段上的动点，当△AOB的面积最大时，则
2-
•
的最小值是（ ）
| AP |
| AO |
| AP |
A、-
| ||||
| B、0 | ||||
C、-
| ||||
D、-
|