题目内容
求满足下列条件的曲线的标准方程:
(1)椭圆C的中心在原点,焦点F1,F2在x轴上,离心率为
.过F1的直线l交C于A,B两点,且△ABF2的周长为16;
(2)焦点在x轴上,焦距为10且点(2,1)在其渐近线上的双曲线方程.
(1)椭圆C的中心在原点,焦点F1,F2在x轴上,离心率为
| ||
| 2 |
(2)焦点在x轴上,焦距为10且点(2,1)在其渐近线上的双曲线方程.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由题意设椭圆方程为
+
=1(a>b>0),由已知得
,由此能求出椭圆方程.
(2)由题意设双曲线方程为
-
=1,a>0,b>0,由已知得
,由此能求出双曲线方程.
| x2 |
| a2 |
| y2 |
| b2 |
|
(2)由题意设双曲线方程为
| x2 |
| a2 |
| y2 |
| b2 |
|
解答:
(本小题满分10分)
解:(1)由题意设椭圆方程为
+
=1(a>b>0),
由已知得
,
解得a=4,b=2
,
∴椭圆方程为
+
=1.…(5分)
(2)由题意设双曲线方程为
-
=1,a>0,b>0,
由已知得
,
解得a=2
,b=
,
∴双曲线方程为
-
=1.…(5分)
解:(1)由题意设椭圆方程为
| x2 |
| a2 |
| y2 |
| b2 |
由已知得
|
解得a=4,b=2
| 2 |
∴椭圆方程为
| x2 |
| 16 |
| y2 |
| 8 |
(2)由题意设双曲线方程为
| x2 |
| a2 |
| y2 |
| b2 |
由已知得
|
解得a=2
| 5 |
| 5 |
∴双曲线方程为
| x2 |
| 20 |
| y2 |
| 5 |
点评:本题考查椭圆方程和双曲线方程的求法,是中档题,解题时要认真审题,注意圆锥曲线的性质的合理运用.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
下列命题中,真命题是( )
| A、?x0∈R,e x0≤0 | ||||||||||||||||
| B、?x∈R,2x>x2 | ||||||||||||||||
| C、“a>1,b>1”是“ab>1”的充要条件 | ||||||||||||||||
D、设
|
已知O为坐标原点,
=(x,y),
=(a,0),
=(0,a),
=(3,4),记|
|、|
|、|
|中的最大值为M,当a取遍一切实数时,M的取值范围是( )
| OP |
| OA |
| OB |
| OC |
| PA |
| PB |
| PC |
A、[
| ||
B、[7+2
| ||
C、[7-2
| ||
D、[7,7+2
|
若直线y=x+b与圆(x-1)2+y2=1有两个不同的公共点,则实数b的取值范围为( )
A、(-
| ||||
B、(-∞,
| ||||
C、(-∞,-
| ||||
D、[-
|
6个同学任意选3个参加一个会议,共有选法种数( )种.
| A、15 | B、10 | C、60 | D、20 |
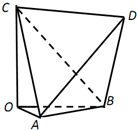 如图,多面体OABCD,AB=CD=2,AD=BC=2
如图,多面体OABCD,AB=CD=2,AD=BC=2