题目内容
已知函数f(x)=2x2+bx+c在(-∞,-
)上减函数,在(-
,+∞)上是增函数,且对应方程两个实根x1,x2满足|x1-x2|=2.
(1)求二次函数的解析式;
(2)求函数f(x)在区间[-2,1]上的值域.
| 3 |
| 2 |
| 3 |
| 2 |
(1)求二次函数的解析式;
(2)求函数f(x)在区间[-2,1]上的值域.
考点:二次函数在闭区间上的最值,函数解析式的求解及常用方法
专题:计算题,函数的性质及应用
分析:(1)由已知可得,对称轴x=-
,求出b,再由韦达定理,即可得到c,进而得到函数的解析式;
(2)考虑对称轴和区间的关系,即可得到最值,进而得到值域.
| 3 |
| 2 |
(2)考虑对称轴和区间的关系,即可得到最值,进而得到值域.
解答:
解:(1)由已知得:对称轴x=-
,
所以-
=-
得b=6,
故f(x)=2x2+6x+c 又x1,x2,是方程2x2+6x+c=0的两个根,
x1+x2=-3,x1x2=
,
所以|x1-x2|=
=
=2,
得c=
,
故f(x)=2x2+6x+
;
(2)f(x)=2x2+6x+
=2(x+
)2-2
当x∈[-2,1]时,f(-
)≤f(x)≤f(1),
即-2≤f(x)≤
,
故值域为[-2,
].
| 3 |
| 2 |
所以-
| b |
| 4 |
| 3 |
| 2 |
故f(x)=2x2+6x+c 又x1,x2,是方程2x2+6x+c=0的两个根,
x1+x2=-3,x1x2=
| c |
| 2 |
所以|x1-x2|=
| (x1+x2)2-4x1x2 |
| 9-2c |
得c=
| 5 |
| 2 |
故f(x)=2x2+6x+
| 5 |
| 2 |
(2)f(x)=2x2+6x+
| 5 |
| 2 |
| 3 |
| 2 |
当x∈[-2,1]时,f(-
| 3 |
| 2 |
即-2≤f(x)≤
| 21 |
| 2 |
故值域为[-2,
| 21 |
| 2 |
点评:本题考查二次函数的解析式的求法,考查二次函数的值域,注意对称轴和区间的关系,考查运算能力,属于中档题.

练习册系列答案
 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
已知an=
(n∈N*),数列{an}的前项和为Sn,则使Sn>0的n最小值( )
| 3 |
| 2n-101 |
| A、99 | B、100 |
| C、101 | D、102 |
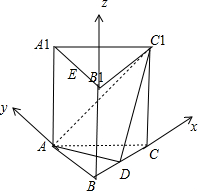 (理)如图,在直三棱柱ABC-A1B1C1中,AB=BC=2AA1=2,∠ABC=90°,D是BC的中点.
(理)如图,在直三棱柱ABC-A1B1C1中,AB=BC=2AA1=2,∠ABC=90°,D是BC的中点.