题目内容
求函数y=（x-5）-2的定义域、单调区间．
考点：函数单调性的判断与证明,函数的定义域及其求法
专题：函数的性质及应用
分析：根据函数y的解析式，求出自变量x的取值范围即可，
再根据函数y的单调性，写出y的单调区间．
再根据函数y的单调性，写出y的单调区间．
解答：
解：∵函数y=（x-5）-2，
∴x-5≠0，
即x≠5，
∴函数y=（x-5）-2的定义域是{x|x≠5}；
又函数y=（x-5）-2图象的对称轴是x=5，
当x＞5时，y随x的增大而减小，是减函数，
当x＜5时，y随x的增大而增大，是增函数，
∴函数y=（x-5）-2的单调增区间是（-∞，5），单调减区间是（5，+∞）．
∴x-5≠0，
即x≠5，
∴函数y=（x-5）-2的定义域是{x|x≠5}；
又函数y=（x-5）-2图象的对称轴是x=5，
当x＞5时，y随x的增大而减小，是减函数，
当x＜5时，y随x的增大而增大，是增函数，
∴函数y=（x-5）-2的单调增区间是（-∞，5），单调减区间是（5，+∞）．
点评：本题考查了求幂函数类型的定义域和单调性的应用问题，是基础题目．
练习册系列答案
相关题目
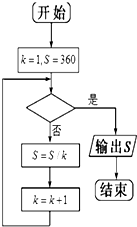执行如图所示的程序框图，运行的结果为S=3，那么判断框中应填入的关于k的判断条件是（ ）| A、k＞6？ | B、k＜6？ |
| C、k＞5？ | D、k＜5？ |
已知函数f（x）的导函数的图象如图所示，则下列判断中正确的是（ ）
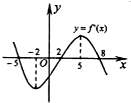
| A、函数f（x）在区间（-2，2）内单调递增 |
| B、函数f（x）在区间（-5，2）内单调递减 |
| C、函数f（x）在区间（5，8）内单调递减 |
| D、函数f（x）在区间（-2，5）内为单调函数 |