题目内容
已知函数f(x)=ln(x+1)+mx(x>-1).
(Ⅰ)若f(x)在x=1的切线平行于x轴,求实数m的值;
(Ⅱ)已知结论:对任意-1<a<b,存在x0∈(a,b),使得f′(x0)=
,求证:函数g(x)=
(x1-x)+f(x1)(其中-1<x1<x2)对任意x1<x<x2,都有f(x)>g(x);
(Ⅲ)已知正数λ1,λ2满足λ1+λ2=1,求证:对任意-1<x1<x2,都有f(λ1x1+λ2x2)>λ1f(x1)+λ2f(x2).
(Ⅰ)若f(x)在x=1的切线平行于x轴,求实数m的值;
(Ⅱ)已知结论:对任意-1<a<b,存在x0∈(a,b),使得f′(x0)=
| f(b)-f(a) |
| b-a |
| f(x2)-f(x1) |
| x2-x1 |
(Ⅲ)已知正数λ1,λ2满足λ1+λ2=1,求证:对任意-1<x1<x2,都有f(λ1x1+λ2x2)>λ1f(x1)+λ2f(x2).
考点:导数在最大值、最小值问题中的应用,利用导数研究曲线上某点切线方程
专题:综合题,导数的综合应用
分析:(Ⅰ)求导函数,利用f(x)在x=1的切线平行于x轴,可得f′(1)=
+m=0,即可求实数m的值;
(Ⅱ)根据f″(x)=-
<0,可得(x)=ln(x+1)+mx是下凸函数,结合函数g(x)=
(x1-x)+f(x1),即可得出结论;
(Ⅲ)利用下凸函数的定义“f(x)是定义在闭区间[a,b]上的函数,若任意x,y∈[a,b]和任意λ∈(0,1),有f(λx+(1-λ)y)≤λf(x)+(1-λ)f(y)成立”进行证明即可.
| 1 |
| 2 |
(Ⅱ)根据f″(x)=-
| 1 |
| (x+1)2 |
| f(x2)-f(x1) |
| x2-x1 |
(Ⅲ)利用下凸函数的定义“f(x)是定义在闭区间[a,b]上的函数,若任意x,y∈[a,b]和任意λ∈(0,1),有f(λx+(1-λ)y)≤λf(x)+(1-λ)f(y)成立”进行证明即可.
解答:
(Ⅰ)解:∵f(x)=ln(x+1)+mx,
∴f′(x)=
+m,
∵f(x)在x=1的切线平行于x轴,
∴f′(1)=
+m=0,
∴m=-
;
(Ⅱ)证明:∵f(x)=ln(x+1)+mx,
∴f′(x)=
+m,
∴f″(x)=-
<0,
∴f(x)=ln(x+1)+mx是下凸函数,
∵函数g(x)=
(x1-x)+f(x1)(其中-1<x1<x2),
∴对任意x1<x<x2,都有f(x)>g(x);
(Ⅲ)证明:根据下凸函数的定义“f(x)是定义在闭区间[a,b]上的函数,若任意x,y∈[a,b]和任意λ∈(0,1),有f(λx+(1-λ)y)≤λf(x)+(1-λ)f(y)成立”
取x=x1,y=x2,λ=λ1,1-λ=1-λ1=λ2,而任意正数λ1,λ2,λ1+λ2=1,x1、x2∈(a,b)
得不等式f(λ1x1+λ2x2)≤λ1f(x1)+λ2f(x2)对于任意的x1,x2∈(a,b)恒成立.
∴f′(x)=
| 1 |
| x+1 |
∵f(x)在x=1的切线平行于x轴,
∴f′(1)=
| 1 |
| 2 |
∴m=-
| 1 |
| 2 |
(Ⅱ)证明:∵f(x)=ln(x+1)+mx,
∴f′(x)=
| 1 |
| x+1 |
∴f″(x)=-
| 1 |
| (x+1)2 |
∴f(x)=ln(x+1)+mx是下凸函数,
∵函数g(x)=
| f(x2)-f(x1) |
| x2-x1 |
∴对任意x1<x<x2,都有f(x)>g(x);
(Ⅲ)证明:根据下凸函数的定义“f(x)是定义在闭区间[a,b]上的函数,若任意x,y∈[a,b]和任意λ∈(0,1),有f(λx+(1-λ)y)≤λf(x)+(1-λ)f(y)成立”
取x=x1,y=x2,λ=λ1,1-λ=1-λ1=λ2,而任意正数λ1,λ2,λ1+λ2=1,x1、x2∈(a,b)
得不等式f(λ1x1+λ2x2)≤λ1f(x1)+λ2f(x2)对于任意的x1,x2∈(a,b)恒成立.
点评:本题主要考查了利用导数研究函数的单调性,以及利用下凸函数的定义证明不等式,属于难题.

练习册系列答案
相关题目
若复数
(a∈R,i为虚数单位)是纯虚数,则实数a的值为( )
| a-i |
| 1+i |
| A、-1 | B、1 | C、2 | D、-2 |
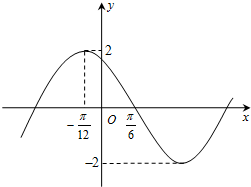 已知函数f(x)=2sin(wx+φ)(其中x∈R,w>0,-π<φ<π)的部分图象如图所示,则函数f(x)的解析式是( )
已知函数f(x)=2sin(wx+φ)(其中x∈R,w>0,-π<φ<π)的部分图象如图所示,则函数f(x)的解析式是( )A、f(x)=2sin(2x-
| ||
B、f(x)=2sin(2x+
| ||
C、f(x)=2sin(6x-
| ||
D、f(x)=2sin(6x+
|
已知函数f(x)=
,则f(2014)=( )
|
| A、2014 | ||
B、
| ||
| C、2015 | ||
D、
|
已知i为虚数单位,a∈R,如果复数2i-
是实数,则a的值为( )
| a |
| 1-i |
| A、-4 | B、2 | C、-2 | D、4 |
已知集合M={x|-2≤x≤8},n={x|x2-3x+2≤0},在集合M中任取一个元素x,则“x∈M∩N”的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|