题目内容
求证:过已知平面外一点且平行于该平面的直线都在过已知点平行于该平面的平面内.
考点:直线与平面平行的性质
专题:空间位置关系与距离
分析:根据条件先出已知,求证,利用反证法即可得到结论.
解答:
 已知:A∉α,A∈a,a∈β,且a∥α,a?β,A∈b,b∥α,
已知:A∉α,A∈a,a∈β,且a∥α,a?β,A∈b,b∥α,
求证:b?β
证明:反证法:
假设b?β,
∵A∈a,A∈b,
∴a∩b=A,
∵a∥α,b∥α且a∩b=A,
∴经过直线a,b的平面γ,满足γ∥α,
又∵β∥α,
∴这与过平面外一点,有且只要一个平面和已知平面平行矛盾,
故假设不成立,
∴恒有b?β成立.
 已知:A∉α,A∈a,a∈β,且a∥α,a?β,A∈b,b∥α,
已知:A∉α,A∈a,a∈β,且a∥α,a?β,A∈b,b∥α,求证:b?β
证明:反证法:
假设b?β,
∵A∈a,A∈b,
∴a∩b=A,
∵a∥α,b∥α且a∩b=A,
∴经过直线a,b的平面γ,满足γ∥α,
又∵β∥α,
∴这与过平面外一点,有且只要一个平面和已知平面平行矛盾,
故假设不成立,
∴恒有b?β成立.
点评:本题主要考查线面平行的判断,利用反证法是解决几何证明题的基本方法.

练习册系列答案
相关题目
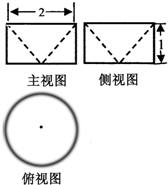 已知某几何体的三视图如图所示,其中俯视图是圆,且该几何体的体积为V1;直径为2的球的体积为V2.则V1:V2=( )
已知某几何体的三视图如图所示,其中俯视图是圆,且该几何体的体积为V1;直径为2的球的体积为V2.则V1:V2=( )| A、1:4 | B、1:2 |
| C、1:1 | D、2:1 |
设m、n是两条不同的直线,α、β是两个不同的平面.下列四个命题中,正确的是( )
| A、α∥β,m?α,n?β,则m∥n |
| B、α⊥β,m⊥β,则m∥α或m?α |
| C、α⊥β,m?α,n?β,则m⊥n |
| D、α∥β,m⊥β,n⊥α,则m∥n |
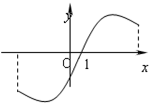 若函数f(x)的图象如图所示,f′(x)是函数f(x)的导函数,且y=f(x+1)是奇函数,则下列结论中
若函数f(x)的图象如图所示,f′(x)是函数f(x)的导函数,且y=f(x+1)是奇函数,则下列结论中