题目内容
设变量x，y满足约束条件
，则目标函数z=2x-3y的最小值为（ ）
|
| A、-4 | B、-2 | C、-1 | D、5 |
考点：简单线性规划
专题：不等式的解法及应用
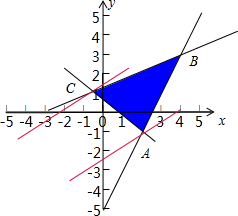
分析：作出题中不等式组表示的平面区域，得如图的△ABC及其内部，再将目标函数z对应的直线进行平移，可得当x=0且y=4时，目标函数取得最小值为-8．
解答：
解：作出不等式组
表示的平面区域：
得到如图的△ABC及其内部，
其中A（2，-1），B（4，3），C（-
，1）
设z=F（x，y）=2x-3y，将直线l：z=2x-3y进行平移，
观察可得：当l经过点C时，目标函数z达到最小值
∴z最小值=F（-
，1）=-4．
故选：A．
解：作出不等式组
|
得到如图的△ABC及其内部，
其中A（2，-1），B（4，3），C（-
| 1 |
| 2 |
设z=F（x，y）=2x-3y，将直线l：z=2x-3y进行平移，
观察可得：当l经过点C时，目标函数z达到最小值
∴z最小值=F（-
| 1 |
| 2 |
故选：A．
点评：本题给出二元一次不等式组，求目标函数的最小值，着重考查了二元一次不等式组表示的平面区域和简单的线性规划等知识，属于中档题．
练习册系列答案
津桥教育计算小状元系列答案
相关题目
通过随机询问250名不同性别的大学生在购买食物时是否看营养说明书，得到如下2×2联表：
从调查的结果分析，认为性别和读营养说明书的关系（ ）
| 女 | 男 | 总计 | |
| 读营养说明书 | 90 | 60 | 150 |
| 不读营养说明书 | 30 | 70 | 100 |
| 总计 | 120 | 130 | 250 |
| A、95%以上认为无关 |
| B、90%～95%认为有关 |
| C、95%～99.9%认为有关 |
| D、99.9%以上认为有关 |
f（x）=2x+3x的一个零点所在的一个区间是 （ ）
| A、（1，2） |
| B、（0，1） |
| C、（-1，0） |
| D、（-2，-1） |
在长方体ABCD-A1B1C1D1中，∠AB1B=45°，∠CB1C1=60°，则异面直线AB1与A1D所成角的余弦值为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
a＞b＞0，下列不等式一定成立的是（ ）
A、a+
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
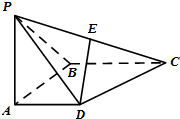如图，在四棱锥P-ABCD中，侧面PAB⊥底面ABCD，且∠PAB=∠ABC=90°，AD∥BC，PA=AB=BC=2AD，E是PC的中点．
如图，在平面直角坐标系xOy中，点A（x1，y1）在单位圆O上，∠xOA=α，且α∈（