题目内容
已知实数x、y满足方程x2+y2-4x+1=0.
(1)求y-x的最大值和最小值;
(2)求x2+y2的最最大值和最小值.
(1)求y-x的最大值和最小值;
(2)求x2+y2的最最大值和最小值.
考点:圆的一般方程
专题:直线与圆
分析:(1)设z=y-x,当点(x,y)在圆(x-2)2+y2=1上,则此直线与圆相切时,z取最值,根据圆心到直线的距离等于半径,求得z的值,即为所求.
(2)根据x2+y2表示点P(x,y)与点O(0,0)间的距离的平方,求出|CO|,再把|CO|加减半径后平方,即得所求.
(2)根据x2+y2表示点P(x,y)与点O(0,0)间的距离的平方,求出|CO|,再把|CO|加减半径后平方,即得所求.
解答:
解:(1)方程x2+y2-4x+1=0 即方程(x-2)2+y2 =3,表示以C(2,0)为圆心、半径等于
的圆.
设z=y-x,当点(x,y)在圆(x-2)2+y2=1上,
使直线z=y-x在y轴上截距最大时,z取得最大值;
使直线z=y-x在y轴上截距最小时,z取得最小值.
则当直线x-y+z=0与圆相切时,z取最值,∵圆心C(2,0),半径r=
,
故当z取得最值时,有
=
,解得z=±
-2,故z=y-x的最大值为
-2,z=y-x的最小值为-2-
.
(2)∵x2+y2表示点P(x,y)与点O(0,0)间的距离的平方.
∵CO=2,x2+y2的最小值为(CO-
)2=(2-
)2=7-4
,最大值为(CO+
)2=(2+
)2=7+4
.
| 3 |
设z=y-x,当点(x,y)在圆(x-2)2+y2=1上,
使直线z=y-x在y轴上截距最大时,z取得最大值;
使直线z=y-x在y轴上截距最小时,z取得最小值.
则当直线x-y+z=0与圆相切时,z取最值,∵圆心C(2,0),半径r=
| 3 |
故当z取得最值时,有
| |2-0+z| | ||
|
| 3 |
| 6 |
| 6 |
| 6 |
(2)∵x2+y2表示点P(x,y)与点O(0,0)间的距离的平方.
∵CO=2,x2+y2的最小值为(CO-
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
点评:题主要考查点到直线的距离公式的应用,直线和圆的位置关系,两点间的距离公式的应用,属于中档题.

练习册系列答案
相关题目
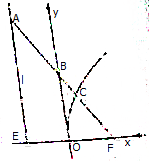 如图,过抛物线y2=2px(p>0)的焦点F的直线分别交抛物线的准线l、y轴、抛物线于A、B、C三点,若
如图,过抛物线y2=2px(p>0)的焦点F的直线分别交抛物线的准线l、y轴、抛物线于A、B、C三点,若| AB |
| BC |
A、-
| ||||
B、-
| ||||
C、-
| ||||
| D、-1 |
设a>0且a≠1,则“函数f(x)=ax在R上是减函数”,是“函数g(x)=(2-a)x3在R上是增函数”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
由点P(2,3)向圆x2+y2=9引切线,则切线长为( )
| A、2 | B、3 | C、4 | D、5 |
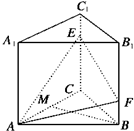 如图,在正三棱柱ABC-A1B1C1中,点E,F分别是棱CC1、BB1上的点,点M是线段AC上的动点,且满足EC=AB=2BF=2cm,当点M在什么位置时,MB∥平面AEF?并求截面AEF的面积.
如图,在正三棱柱ABC-A1B1C1中,点E,F分别是棱CC1、BB1上的点,点M是线段AC上的动点,且满足EC=AB=2BF=2cm,当点M在什么位置时,MB∥平面AEF?并求截面AEF的面积.