题目内容
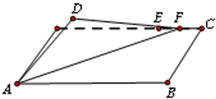 如图,在长方形ABCD中,AB=4,BC=1,E为DC的四等分点(靠近C处),F为线段EC上一动点(包括端点),现将△AFD沿AF折起,使D点在平面内的射影恰好落在边AB上,则当F运动时,二面角D-AF-B的平面角余弦值的变化范围为
如图,在长方形ABCD中,AB=4,BC=1,E为DC的四等分点(靠近C处),F为线段EC上一动点(包括端点),现将△AFD沿AF折起,使D点在平面内的射影恰好落在边AB上,则当F运动时,二面角D-AF-B的平面角余弦值的变化范围为考点:二面角的平面角及求法
专题:空间位置关系与距离
分析:过点D作DM⊥AF于点O,交AB于点M,不妨设二面角D-AF-B的平面解为θ,则cosθ=
=
=
,从而求其取值范围.
| MO |
| OD |
| OA |
| OF |
| 1 |
| x2 |
解答:
解:如图,过点D作DM⊥AF于点O,交AB于点M,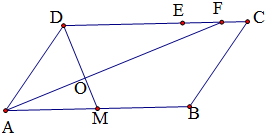 不妨设二面角D-AF-B的平面解为θ,
不妨设二面角D-AF-B的平面解为θ,
则cosθ=
,
设DF=x,3≤x≤4,由勾股定理,
OD=
,OF=
,OA=
,
∴cosθ=
=
=
在[3,4]上是减函数,
∴
cosθ≤
.
故答案为:[
,
].
 不妨设二面角D-AF-B的平面解为θ,
不妨设二面角D-AF-B的平面解为θ,则cosθ=
| OM |
| OD |
设DF=x,3≤x≤4,由勾股定理,
OD=
| x | ||
|
|
|
∴cosθ=
| MO |
| OD |
| OA |
| OF |
| 1 |
| x2 |
∴
| 1 |
| 16 |
| 1 |
| 9 |
故答案为:[
| 1 |
| 16 |
| 1 |
| 9 |
点评:本题考查了学生的作图能力及空间想象力,注意折起前后的等量关系是本题解决的关键,属于中档题.

练习册系列答案
相关题目

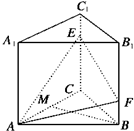 如图,在正三棱柱ABC-A1B1C1中,点E,F分别是棱CC1、BB1上的点,点M是线段AC上的动点,且满足EC=AB=2BF=2cm,当点M在什么位置时,MB∥平面AEF?并求截面AEF的面积.
如图,在正三棱柱ABC-A1B1C1中,点E,F分别是棱CC1、BB1上的点,点M是线段AC上的动点,且满足EC=AB=2BF=2cm,当点M在什么位置时,MB∥平面AEF?并求截面AEF的面积.