题目内容
定义运算A
=x(x-1)(x-2)…(x-m+1),其中x∈R,m∈N,已知函数f(x)=aA
-12A
+1,(a∈R,且a≠0)在x=1处取得极值,且方程f(x)=6x-
在区间(m,m+1)(m∈N*)内有且只有两两不相等的实数根,则(1)实数a的值为 ;(2)正整数m的值为 .
m x |
3 x+1 |
2 x |
| 16 |
| x |
考点:利用导数研究函数的极值
专题:计算题,函数的性质及应用,导数的综合应用
分析:由题意,设f(x)=a(x+1)x(x-1)-12x(x-1)+1=ax3-12x2-(a-12)x+1,求导并令导数为0即可求a,再化简方程f(x)=6x-
等价于18x3-36x2+19=0,从而令g(x)=18x3-36x2+19,求导判断函数的单调性及极值点,从而求得m的值.
| 16 |
| 3 |
解答:
解:由题意,设f(x)=a(x+1)x(x-1)-12x(x-1)+1=ax3-12x2-(a-12)x+1,
∴f′(x)=3ax2-24x-(a-12),
f′(1)=3a-24-(a-12)=0,
故a=6;
方程f(x)=6x-
等价于18x3-36x2+19=0.
令g(x)=18x3-36x2+19.
则g'(x)=54x2-72x=18x(3x-4),
令g'(x)=0得x=0或x=
;
当x∈(0,
)时,g'(x)<0,g(x)是单调递减函数;
当x∈(
,+∞)时,g'(x)>0,g(x)是单调递增函数;
∵g(1)=1>0,g(
)=-
<0,g(2)=19>0,
∴方程g(x)=0在区间(1,
),(
,2)内分别有唯一实根;
∴存在正整数m=1使得方程f(x)=6x-
在区间(1,2)上有且只有两个不相等的实数根;
故答案为:6,1.
∴f′(x)=3ax2-24x-(a-12),
f′(1)=3a-24-(a-12)=0,
故a=6;
方程f(x)=6x-
| 16 |
| 3 |
令g(x)=18x3-36x2+19.
则g'(x)=54x2-72x=18x(3x-4),
令g'(x)=0得x=0或x=
| 4 |
| 3 |
当x∈(0,
| 4 |
| 3 |
当x∈(
| 4 |
| 3 |
∵g(1)=1>0,g(
| 4 |
| 3 |
| 7 |
| 3 |
∴方程g(x)=0在区间(1,
| 4 |
| 3 |
| 4 |
| 3 |
∴存在正整数m=1使得方程f(x)=6x-
| 16 |
| 3 |
故答案为:6,1.
点评:本题考查了导数的综合应用及函数的零点的个数的判断,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
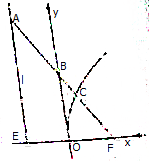 如图,过抛物线y2=2px(p>0)的焦点F的直线分别交抛物线的准线l、y轴、抛物线于A、B、C三点,若
如图,过抛物线y2=2px(p>0)的焦点F的直线分别交抛物线的准线l、y轴、抛物线于A、B、C三点,若| AB |
| BC |
A、-
| ||||
B、-
| ||||
C、-
| ||||
| D、-1 |
设a>0且a≠1,则“函数f(x)=ax在R上是减函数”,是“函数g(x)=(2-a)x3在R上是增函数”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
下列判断中正确的是( )
| A、?m∈R使f(x)=(m-1)x m2-4m+3是幂函数,且在(0,+∞)上递减 | ||||||
B、“
| ||||||
C、命题“若a+
| ||||||
| D、命题“?a∈R,a2+1≥2a”的否定是:“?a∈R,a2+1≤2a” |