题目内容

已知函数f（x）=logax的反函数的图象过点（4，4），则a=
 
．
考点：反函数
专题：函数的性质及应用
分析：由题意可得loga4=4，化为指数式可解得a值．
解答： 解：∵函数f（x）=logax的反函数的图象过点（4，4），
∴函数f（x）=logax的图象过点（4，4）关于y=x的对称点（4，4），
∴f（4）=loga4=4，即a4=4，解得a=
2

故答案为：
2
点评：本题考查反函数，涉及对数的运算，属基础题．
练习册系列答案
相关题目
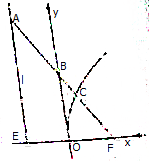如图，过抛物线y2=2px（p＞0）的焦点F的直线分别交抛物线的准线l、y轴、抛物线于A、B、C三点，若
AB
=3
BC
，则直线AF的斜率是（　　）
A、-
3
B、-
3
3
C、-
2
2
D、-1
已知非零向量
e1
、
e2
不共线，如果
AB
=
e1
+
e2
，
AC
=2
e1
+8
e2
，
AD
=3
e1
-3
e2
，求证：A、B、C、D共面．
已知f（x）=
a
•
b
-1，其中向量
a
=（
3
sin2x，cosx），
b
=（1，2cosx），x∈[0，
π
2
]，则f（x）的单调递减区间为
 
．
有下列四个命题：
①5≥2且7≥3；
②平行四边形的对角线互相垂直或平分；
③若x+y≠3，则x≠1或y≠2；
④若（x-1）（x-2）=0，则x=1．
其中真命题为
 
．（填上你认为正确的命题序号）
在△ABC中，tan
A+B
2
=2sinC，若AB=1，则
1
2
AC+BC的最大值为
 
．
下列判断中正确的是（　　）
A、?m∈R使f（x）=（m-1）x m2-4m+3是幂函数，且在（0，+∞）上递减
B、“
1
a
+
1
b
=4”的必要不充分条件是“a=b=
1
2
”
C、命题“若a+
1
a
=2，则a=1”的逆否命题是“若a=1则a+
1
a
≠2”
D、命题“?a∈R，a2+1≥2a”的否定是：“?a∈R，a2+1≤2a”
由点P（2，3）向圆x2+y2=9引切线，则切线长为（　　）
A、2B、3C、4D、5
在△ABC中，∠ACB=90°，AC=BC=2，点P是AB上的一个三等分点，则
CP
•
CB
+
CP
•
CA
=（　　）
A、4B、1C、0D、-3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网