题目内容
若n为大于1的自然数,求证
+
+…+
>
.
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| 2n |
| 7 |
| 13 |
考点:不等式的证明
专题:数学模型法,函数的性质及应用,不等式的解法及应用
分析:本题可以先构造关于n的函数,研究其单调性,得到其最小值,从而得出本题结论.
解答:
解:记f(n)=
+
+…+
,n∈N.
∵f(n+1)-f(n)=
+
+…+
+
-(
+
+…+
)
=
+
-
=
>0,
∴f(n+1)>f(n),
即f(n)在自然数集上单调递增.
∵n为大于1的自然数,
∴f(n)≥f(2)=
+
=
>
.
∴
+
+…+
>
.
故原不等式成立.
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| 2n |
∵f(n+1)-f(n)=
| 1 |
| n+2 |
| 1 |
| n+3 |
| 1 |
| 2n+1 |
| 1 |
| 2n+2 |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| 2n |
=
| 1 |
| 2n+1 |
| 1 |
| 2n+2 |
| 1 |
| n+1 |
| 1 |
| (2n+1)(2n+2) |
∴f(n+1)>f(n),
即f(n)在自然数集上单调递增.
∵n为大于1的自然数,
∴f(n)≥f(2)=
| 1 |
| 3 |
| 1 |
| 4 |
| 7 |
| 12 |
| 7 |
| 13 |
∴
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| 2n |
| 7 |
| 13 |
故原不等式成立.
点评:本题考查的是构造函数法、放缩法证明不等式,本题有一定的难度,属于中档题.

练习册系列答案
相关题目
 一个容量为M的样本数据,其频率分布表如下.
一个容量为M的样本数据,其频率分布表如下.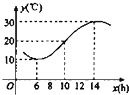 某地一填从6时至14时的温度函数变化曲线近似满足y=Asin(ωx+φ)+b(|φ|<π)
某地一填从6时至14时的温度函数变化曲线近似满足y=Asin(ωx+φ)+b(|φ|<π)