题目内容
 一个容量为M的样本数据,其频率分布表如下.
一个容量为M的样本数据,其频率分布表如下.(1)求a,b的值,并画出频率分布直方图;(答案写在答题卡上)
(2)用频率分布直方图,求出总体的众数、中位数及平均数的估计值.
频率分布表
| 分组 | 频数 | 频率 | 频率/组距 |
| (10,20] | 2 | 0.10 | 0.010 |
| (20,30] | 3 | 0.15 | 0.015 |
| (30,40] | 4 | 0.20 | 0.020 |
| (40,50] | a | b | 0.025 |
| (50,60] | 4 | 0.20 | 0.020 |
| (60,70] | 2 | 0.10 | 0.010 |
考点:频率分布直方图
专题:概率与统计
分析:(1)根据各组累积频率为1,可求出b,由样本容量=
,求出M,结合b值,可得a值,再由矩形的高=
计算各组矩形的高,可得频率分布直方图;
(2)在频率分布直方图中,众数是最高的小长方形的底边的中点横坐标的值,中位数是所有小长方形的面积相等的分界线,平均数是各小长方形底边中点的横坐标与对应频率的积的和,由此求出即可.
| 频数 |
| 频率 |
| 频率 |
| 组距 |
(2)在频率分布直方图中,众数是最高的小长方形的底边的中点横坐标的值,中位数是所有小长方形的面积相等的分界线,平均数是各小长方形底边中点的横坐标与对应频率的积的和,由此求出即可.
解答:
解:(1)∵各组累积频率为1,
∴b=1-(0.10+0.15+0.20+0.20+0.10)=0.25,
由第组的频数为2,频率为0.10,
故样本容量M=
=20,
故a=20×0.25=5,-------(2分)
频率分布直方图如下图所示:

(2)由第四组的频率最大,
可得:众数约为第四组的组中值45-------------(8分);
由前三组的累积频率为:0.10+0.15+0.20=0.45<0.50,
前四组的累积频率为:0.10+0.15+0.20+0.25=0.70>0.50,
故数据的中位数约为:40+10×
=42-----------(10分);
数据的平均数约为:15×0.1+25×0.15+35×0.2+45×0.25+55×0.2+65×0.1=41-----(12分)
∴b=1-(0.10+0.15+0.20+0.20+0.10)=0.25,
由第组的频数为2,频率为0.10,
故样本容量M=
| 2 |
| 0.10 |
故a=20×0.25=5,-------(2分)
频率分布直方图如下图所示:

(2)由第四组的频率最大,
可得:众数约为第四组的组中值45-------------(8分);
由前三组的累积频率为:0.10+0.15+0.20=0.45<0.50,
前四组的累积频率为:0.10+0.15+0.20+0.25=0.70>0.50,
故数据的中位数约为:40+10×
| 1 |
| 5 |
数据的平均数约为:15×0.1+25×0.15+35×0.2+45×0.25+55×0.2+65×0.1=41-----(12分)
点评:本题利用频率分布直方图,考查了求数据的众数、中位数和平均数的问题,解题时应根据众数、中位数以及平均数的意义,分别求出它们,是比较基础题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 如图,点A在直线x=5上移动,等腰△OPA的顶角∠OPA为120°(O,P,A按顺时针方向排列),求点P极坐标系的轨迹方程,并化成直角坐标系方程.
如图,点A在直线x=5上移动,等腰△OPA的顶角∠OPA为120°(O,P,A按顺时针方向排列),求点P极坐标系的轨迹方程,并化成直角坐标系方程.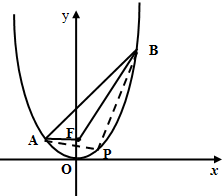 如图,已知抛物线x2=4y上两定点A,B分别在对称轴左、右两侧,F为抛物线的焦点,且|AF|=2,|BF|=5.
如图,已知抛物线x2=4y上两定点A,B分别在对称轴左、右两侧,F为抛物线的焦点,且|AF|=2,|BF|=5.