题目内容
求下列函数的导数:
(1)y=(1+2x2)8;
(2)y=
;
(3)y=sin 2x-cos 2x;
(4)y=cos x2.
(1)y=(1+2x2)8;
(2)y=
| 1 | ||
|
(3)y=sin 2x-cos 2x;
(4)y=cos x2.
考点:导数的运算
专题:导数的概念及应用
分析:根据导数的运算法则和导数的公式即可得到结论.
解答:
解 (1)设y=u8,u=1+2x2,
∴y′=(u8)′(1+2x2)′=8u7•4x=8(1+2x2)7•4x=32x(1+2x2)7.
(2)设y=u-
,u=1-x2,
则y′=(u-
)′(1-x2)′=(-
u-
)•(-2x)=x(1-x2)-
.
(3)y′=(sin 2x-cos 2x)′=(sin 2x)′-(cos 2x)′=2cos 2x+2sin 2x=2
sin (2x+
).
(4)设y=cos u,u=x2,则y′=(cos u)′•(x2)′=(-sin u)•2x=(-sin x2)•2x=-2xsin x2.
∴y′=(u8)′(1+2x2)′=8u7•4x=8(1+2x2)7•4x=32x(1+2x2)7.
(2)设y=u-
| 1 |
| 2 |
则y′=(u-
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
(3)y′=(sin 2x-cos 2x)′=(sin 2x)′-(cos 2x)′=2cos 2x+2sin 2x=2
| 2 |
| π |
| 4 |
(4)设y=cos u,u=x2,则y′=(cos u)′•(x2)′=(-sin u)•2x=(-sin x2)•2x=-2xsin x2.
点评:本题主要考查导数的计算,要求熟练掌握常见函数的导数公式和导数的运算法则.

练习册系列答案
相关题目
设f(x),g(x)分别是定义在R上的奇函数和偶函数,当x<0时,f′(x)g(x)+f(x)g′(x)<0,且g(-2)=0,则不等式f(x)g(x)>0的解集是( )
| A、(-2,0)∪(2,+∞) |
| B、(-∞,-2)∪(2,+∞) |
| C、(-∞,-2)∪(0,2) |
| D、(-2,0)∪(0,2) |
已知函数f(x)=cosxsin2x,下列结论中不正确的是( )
| A、y=f(x)的图象关于(π,0)中心对称 | ||||
B、y=f(x)的图象关于x=
| ||||
C、f(x)的最大值为
| ||||
| D、f(x)既是奇函数,又是周期函数 |
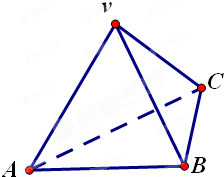 如图,在三棱锥V-ABC中,VA=VB=AC=BC=2,AB=2
如图,在三棱锥V-ABC中,VA=VB=AC=BC=2,AB=2