题目内容
已知圆C:x2+y2-2x-4=0一条斜率等于1的直线l与圆C交于A,B两点,
(1)求弦AB最长时直线l的方程;
(2)求△ABC面积最大时直线l的方程;
(3)若坐标原点O在以AB为直径的圆内,求直线l在y轴上的截距范围.
(1)求弦AB最长时直线l的方程;
(2)求△ABC面积最大时直线l的方程;
(3)若坐标原点O在以AB为直径的圆内,求直线l在y轴上的截距范围.
考点:直线和圆的方程的应用
专题:综合题,直线与圆
分析:(1)欲求弦AB最长时直线L的方程,依据圆的特征:圆的直径是最长的弦,只须求出l过圆心时的方程即可;
(2)欲求△ABC面积最大时直线L的方程,因其两腰定长,故只须顶角为直角时面积最大,最后利用点到直线的距离公式求解即可;
(3)由斜率为1设出直线l方程y=x+b,表示过C且与直线l垂直的直线方程,两方程联立,求出方程组的解,即为以AB为直径的圆心坐标D,再利用点到直线的距离公式表示出圆心C到直线l的距离d,利用垂径定理及勾股定理表示出DA2,即为以AB为直径圆的半径平方,表示出圆D的方程,原点O在圆内,得到圆心D到原点距离小于圆的半径,列出关于b的不等式,求出不等式的解集得到b的范围,即为直线l在y轴上截距的范围.
(2)欲求△ABC面积最大时直线L的方程,因其两腰定长,故只须顶角为直角时面积最大,最后利用点到直线的距离公式求解即可;
(3)由斜率为1设出直线l方程y=x+b,表示过C且与直线l垂直的直线方程,两方程联立,求出方程组的解,即为以AB为直径的圆心坐标D,再利用点到直线的距离公式表示出圆心C到直线l的距离d,利用垂径定理及勾股定理表示出DA2,即为以AB为直径圆的半径平方,表示出圆D的方程,原点O在圆内,得到圆心D到原点距离小于圆的半径,列出关于b的不等式,求出不等式的解集得到b的范围,即为直线l在y轴上截距的范围.
解答:
解:(1)∵L过圆心时弦长AB最大,圆心坐标为(1,-2),∴L的方程为x-y-3=0;
(2)△ABC的面积S=
CA•CBsin∠ACB=
sin∠ACB,
当∠ACB=
时,△ABC的面积S最大,
此时△ABC为等腰三角形;
设L方程为y=x+m,则圆心到直线距离为
,
从而有
=
,
m=0或m=-6,
则L方程为x-y=0或x-y-6=0.
(3)可设直线l:y=x+b,
过点C(1,0)与l垂直的直线的方程为y=-(x-1),即x+y-1=0,
由
,解得:
,即以AB为直径的圆的圆心坐标为D(
,
),
圆心C到直线l的距离d=
,
而DA2=CA2-d2=5-
,
以AB为直径的圆D:(x-
)2+(y-
)2=5-
,
点O在以AB为直径的圆D内,即(
)2+(
)2<5-
,
解得:
<b<
,
则所求直线l在y轴上的截距范围为(
,
).
(2)△ABC的面积S=
| 1 |
| 2 |
| 9 |
| 2 |
当∠ACB=
| π |
| 2 |
此时△ABC为等腰三角形;
设L方程为y=x+m,则圆心到直线距离为
3
| ||
| 2 |
从而有
| |1+2+m| | ||
|
3
| ||
| 2 |
m=0或m=-6,
则L方程为x-y=0或x-y-6=0.
(3)可设直线l:y=x+b,
过点C(1,0)与l垂直的直线的方程为y=-(x-1),即x+y-1=0,
由
|
|
| 1-b |
| 2 |
| 1+b |
| 2 |
圆心C到直线l的距离d=
| |1+b| | ||
|
而DA2=CA2-d2=5-
| (1+b)2 |
| 2 |
以AB为直径的圆D:(x-
| 1-b |
| 2 |
| 1+b |
| 2 |
| (1+b)2 |
| 2 |
点O在以AB为直径的圆D内,即(
| 1-b |
| 2 |
| 1+b |
| 2 |
| (1+b)2 |
| 2 |
解得:
-1-
| ||
| 2 |
-1+
| ||
| 2 |
则所求直线l在y轴上的截距范围为(
-1-
| ||
| 2 |
-1+
| ||
| 2 |
点评:本小题主要考查直线的一般式方程、直线和圆的方程的应用、点到直线的距离公式等基础知识,考查运算求解能力,考查数形结合思想、函数与方程思想、化归与转化思想.属于中档题.

练习册系列答案
相关题目
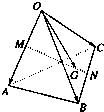 (B题)已知空间四边形OABC,M、N分别是对边OA、BC的中点,点G在线段MN上,且
(B题)已知空间四边形OABC,M、N分别是对边OA、BC的中点,点G在线段MN上,且| MG |
| GN |
| OG |
| OA |
| OB |
| OC |
A、x=
| ||||||
B、x=
| ||||||
C、x=
| ||||||
D、x=
|
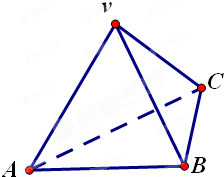 如图,在三棱锥V-ABC中,VA=VB=AC=BC=2,AB=2
如图,在三棱锥V-ABC中,VA=VB=AC=BC=2,AB=2