题目内容
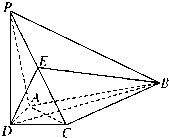如图，在四棱锥P-ABCD中，PD⊥平面ABCD，AD=CD，DB平分∠ADC，E为PC的中点．（Ⅰ）证明：PA∥平面BDE；
（Ⅱ）证明：AC⊥平面PBD．
考点：直线与平面平行的判定,直线与平面垂直的判定
专题：空间位置关系与距离
分析：（Ⅰ）设AC∩BD=H，连结EH．证明EH∥PA．利用直线与平面的平行的判定定理证明PA∥平面BDE．
（Ⅱ）通过PD⊥平面ABCD，证明PD⊥AC．结合DB⊥AC．然后证明AC⊥平面PBD
（Ⅱ）通过PD⊥平面ABCD，证明PD⊥AC．结合DB⊥AC．然后证明AC⊥平面PBD
解答：
（Ⅰ）证明：设AC∩BD=H，连结EH．
在△ADC中，∵AD=CD，且DB平分∠ADC，
∴H为AC的中点．
又由题设，E为PC的中点，故EH∥PA．
又EH⊆平面BDE，且PA?平面BDE，
∴PA∥平面BDE．…（6分）
（Ⅱ）证明：∵PD⊥平面ABCD，AC⊆平面ABCD，∴PD⊥AC．
由（1）可得，DB⊥AC．
又PD∩DB=D，故AC⊥平面PBD．…（12分）
在△ADC中，∵AD=CD，且DB平分∠ADC，
∴H为AC的中点．
又由题设，E为PC的中点，故EH∥PA．
又EH⊆平面BDE，且PA?平面BDE，
∴PA∥平面BDE．…（6分）
（Ⅱ）证明：∵PD⊥平面ABCD，AC⊆平面ABCD，∴PD⊥AC．
由（1）可得，DB⊥AC．
又PD∩DB=D，故AC⊥平面PBD．…（12分）
点评：本题考查直线与平面的平行的判定定理以及在与平面垂直的判定定理的应用，考查逻辑推理能力．
练习册系列答案
相关题目
设α是空间中的一个平面，l，m，n是三条不同的直线，则下列命题中正确的是（ ）
| A、若m?α，n?α，l⊥m，l⊥n，则l⊥α |
| B、若m?α，n⊥α，l⊥n，则l∥m |
| C、若l⊥m，l⊥n，则n∥m |
| D、若m⊥α，n⊥α，则n∥m |
已知点P，A，B在双曲线
-
=1上，直线AB过坐标原点，且直线PA、PB的斜率之积为
，则双曲线的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 3 |
A、
| ||||
B、
| ||||
| C、2 | ||||
D、
|
设全集U={1，2，3，4，5，}，M={1，2，}则∁UM=（ ）
| A、{3} |
| B、{4，5} |
| C、{3，4，5} |
| D、（4，5） |