题目内容
在小于100的自然数中，所有被7除余2的数之和为（ ）
| A、765 | B、665 |
| C、763 | D、663 |
考点：等差数列的前n项和,等差数列的通项公式
专题：等差数列与等比数列
分析：由题意列式求出满足条件的项的项数，然后利用等差数列的求和公式求解．
解答：
解：由7n+2＜100，得n＜14，
∴n的取值为从0到13，
∴在小于100的自然数中，所有被7除余2的数构成以2为首项，以7为公差的等差数列，
其和为s=14×2+
=665．
故选：B．
∴n的取值为从0到13，
∴在小于100的自然数中，所有被7除余2的数构成以2为首项，以7为公差的等差数列，
其和为s=14×2+
| 14×(14-1)×7 |
| 2 |
故选：B．
点评：本题考查了等差数列的通项公式，考查了等差数列的前n项和的求法，是基础的计算题．
练习册系列答案
相关题目
如果α在第二象限，则
必定在（ ）
| α |
| 2 |
| A、第一或第二象限 |
| B、第一或第三象限 |
| C、第三或第四象限 |
| D、第二或第四象限 |
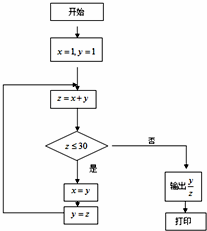
如图所示计算机程序的打印结果为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
给出命题：若cosα=
，则α=
．在它的逆命题、否命题、逆否命题三个命题中，真命题的个数是（ ）
| 1 |
| 2 |
| π |
| 3 |
| A、3 | B、2 | C、1 | D、0 |
过点A（2，b）和点B（3，-2）的直线的倾斜角为
，则b的值是（ ）
| 3π |
| 4 |
| A、-1 | B、1 | C、-5 | D、5 |
在平面直角坐标系xOy中，已知平面向量
=（a，0），
=（0，b），其中a，b为[-2，2]上的两个随机实数，定义平面上的点集Ω，Ω1，Φ分别为Ω={P|
=
+
}，Ω1={Q|
|=|
|=
且|QP|＜1，P∈Ω}，Φ：Ω1∪{R|
＜|
|＜2}．若在Ω对应的平面区域内随机取一个点W，则点W落在Φ对应的平面区域内的概率为（ ）
| ON1 |
| ON2 |
| OP |
| ON1 |
| ON2 |
| QN1 |
| QN2 |
| 2 |
| 3 |
| OR |
A、
| ||
B、1-
| ||
C、
| ||
D、
|
若x=
，则sin4x-cos4x的值为（ ）
| π |
| 12 |
A、
| ||||
B、-
| ||||
C、-
| ||||
D、
|