题目内容
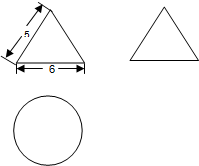一个几何体的三视图及其尺寸如下（单位cm），则该几何体的表面积及体积为（cm2\cm3）（ ）| A、24π，12π |
| B、15π，12π |
| C、24π，36π |
| D、以上都不正确 |
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：由已知中的三视图及其尺寸，我们易判断这个几何体是圆锥，且底面直径为6，圆锥的母线长为5，代入圆锥的表面积和体积公式，我们易得结论．
解答：
解：由三视图可得该几何体为圆锥，且底面直径为6，即底面半径为r=3，圆锥的母线长l=5，
则圆锥的底面积S底面=π•r2=9π
侧面积S侧面=π•r•l=15π，
故几何体的表面积S=9π+15π=24πcm2，
又由圆锥的高h=
=4，
故V=
•S底面•h=12πcm3．
故选A．
则圆锥的底面积S底面=π•r2=9π
侧面积S侧面=π•r•l=15π，
故几何体的表面积S=9π+15π=24πcm2，
又由圆锥的高h=
| l2-r2 |
故V=
| 1 |
| 3 |
故选A．
点评：本题考查的知识点是由三视图求面积和体积，根据三视图判断几何体的底面半径和母线长是解答本题的关键．
练习册系列答案
同步练习强化拓展系列答案
相关题目
已知0＜x＜4.5，当x2（9-2x）取得最大值时，x取何值（ ）
| A、1 | B、2 | C、3 | D、27 |
如果α在第二象限，则
必定在（ ）
| α |
| 2 |
| A、第一或第二象限 |
| B、第一或第三象限 |
| C、第三或第四象限 |
| D、第二或第四象限 |
设全集 U={1，2，3，4，5，6，7}，M={2，3，4，6}，N={1，4，5}，则（∁UM）∩N 等于（ ）
| A、{1，2，4，5，7} |
| B、{1，4，5} |
| C、{1，5} |
| D、{1，4} |
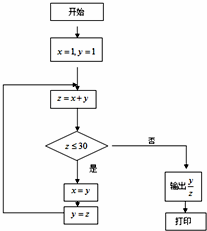
如图所示计算机程序的打印结果为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
给出命题：若cosα=
，则α=
．在它的逆命题、否命题、逆否命题三个命题中，真命题的个数是（ ）
| 1 |
| 2 |
| π |
| 3 |
| A、3 | B、2 | C、1 | D、0 |
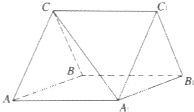如图，三棱柱ABC-A1B1C1中，CA=CB，AB=AA1，∠BAA1=60°．