如图.网格纸上小正方形的边长为1.粗线画出的是某几何体的三视图.则该几何体的表面积为( )A．$\frac{8}{3}$+2πB．4+4$\sqrt{2}$+3πC．8+4$\sqrt{2}$+3πD．10+4$\sqrt{2}$+2π 题目和参考答案——青夏教育精英家教网—

题目内容

3．如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则该几何体的表面积为（　　）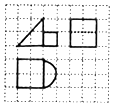

A．

$\frac{8}{3}$+2π

B．

4+4$\sqrt{2}$+3π

C．

8+4$\sqrt{2}$+3π

D．

10+4$\sqrt{2}$+2π

分析首先由三视图还原几何体，然后计算表面积．

解答解：由已知得到几何体为一个三棱柱与一个半圆柱的组合，
其中三棱柱的高为2，底为一个等腰直角三角形，腰长为2；
半圆柱的高为1，底面是半径为1的半圆．所以表面积为$\frac{1}{2}×2×2×2+2\sqrt{2}×2+2×2+π×{1^2}+2×1+π×1×1=10+4\sqrt{2}+2π$．
故选D．

点评本题考査空间几何体的表面积．关键是明确几何体的形状．

练习册系列答案

	A．	如果不买彩票，那么就不能中奖，因为你买了彩票，所以你一定中奖
	B．	因为a＞b，a＞c，所以a-b＞a-c
	C．	若a，b均为正实数，则lga+lgb≥2$\sqrt{lga•lgb}$
	D．	若ab＜0，则$\frac{a}{b}$+$\frac{b}{a}$=-[（-$\frac{a}{b}$）+（-$\frac{b}{a}$）]≤-2$\sqrt{（-\frac{a}{b}）（-\frac{b}{a}）}$≤-2

11．在空间直角坐标系中，点A（1，0，1）和点B（2，1，-1）间的距离$\sqrt{6}$．

18．已知角α=390°
（1）角α的终边在第几象限；
（2）写出与角α终边相同的角的集合；
（3）在-360°～720°范围内，写出与α终边相同的角．

8．已知一个几何体的三视图如图所示（单位：cm），则该几何体的体积为$\frac{10}{3}$cm³．